2020-06-08
1624
Рассмотрим траекторию движения точки (рис. 10.13). Положение точки 
на траектории будем определять дуговой координатой 
, отсчитываемой от произвольно выбранной на траектории неподвижной точки 
.
рис. 9
Проведем через точку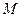 
касательную к траектории и будем определять положительное направление этой касательной единичным вектором 
, направленным по касательной в сторону возрастания дуговой координаты и равным по модулю единице. Этот вектор называется ортом касательной. Если провести через точку 
плоскость, перпендикулярную к касательной в этой точке, то такая плоскость называется нормальной (рис. 9). Любая прямая, проведенная через точку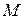 
в нормальной плоскости, перпендикулярна к касательной 
и является нормалью траектории в точке 
.
Теперь возьмем на траектории точку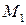 
, близкую к точке 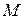(рис. 9). Орт касательной в этой точке обозначим 
. Построим плоскость, проходящую через два вектора 
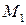и , а затем будем точку неограниченно приближать к точке 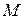так, чтобы в пределе эти точки совпали. Так как при этом направление вектора будет изменяться, то будет изменяться и положение этой плоскости. Очевидно, что она будет вращаться вокруг вектора , приближаясь к некоторому предельному положению. Плоскость, представляющая собой предельное положение плоскости, построенной на векторах и , при стремлении точки 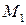к точке , называется соприкасающейся плоскостью данной кривой в точке (рис. 9). Из этого определения следует, что касательная в точке лежит в соприкасающейся плоскости и для случая плоской траектории соприкасающаяся плоскость совпадает с той плоскостью, в которой расположена эта траектория.
Нормаль, лежащая в соприкасающейся плоскости, т.е. линия пересечения нормальной и соприкасающихся плоскостей, называется главной нормалью данной кривой в точке .
За положительное направление главной нормали принимается направление от точки в сторону вогнутости траектории, и это направление определяют единичным вектором 
. Вектор называется ортом главной нормали (рис. 9). Нормаль, перпендикулярная к соприкасающейся плоскости, называется бинормалью, а ее направление определяется орт вектором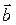 
(рис. 9). Плоскость, построенная на касательной и бинормали, называется спрямляющей плоскостью.
Три оси, имеющие начало в точке 
и направленные по касательной, главной нормали и бинормали к траектории в этой точке, называются естественными осями и являются ребрами триэдра, или естественного трехгранника.
Естественный трехгранник представляет собой прямоугольную систему координат, отличающуюся от декартовой тем, что за начало координат здесь принимается движущаяся точка, т.е. естественный трехгранник с течением времени меняет свое положение в пространстве, двигаясь с точкой .
