Задание 9. Теоретические вопросы.
- Если
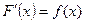 , то функция F(х) называется …?
, то функция F(х) называется …? - Совокупность всех первообразных функций называется...?
- Определенный интеграл с равными пределами интегрирования равен …
- Формула Ньютона-Лейбница вычисляет …
- Операция нахождения первообразных по данной функции называется …
- Свойства интегралов.
Задание 10. Метод непосредственного интегрирования неопределенного интеграла.
- Множество всех первообразных функции
 имеет вид …,
имеет вид …, -
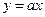 ,
, -
 .
. - Неопределенный интеграл
 равен …,
равен …, -
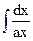 .
.
Задание 11. Интегрирование неопределенного интеграла методом замены переменных.
- Неопределенный интеграл
 равен …
равен … - В результате подстановки
 интеграл
интеграл  приводится к виду …
приводится к виду … - В результате подстановки
 интеграл
интеграл 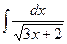 приводится к виду …
приводится к виду … - В результате подстановки
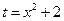 интеграл
интеграл 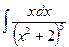 приводится к виду …
приводится к виду … - Неопределенный интеграл
 равен …
равен …
Задание 12. Определенный интеграл. Формула Ньютона – Лейбница.
-

-
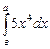 ,
, -
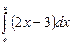 ,
, -
 ,
, -
 ,
, -
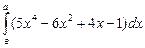 ,
, -
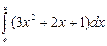 ,
, -
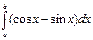 ,
, -
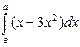 .
.
Задание 13. Замена переменной в определенном интеграле.
-
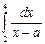 ,
, -
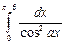 ,
, -
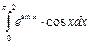
-
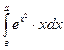 ,
, -
 ,
, -

Задание 14. Геометрические приложения определенного интеграла.
- Площадь криволинейной трапеции D определяется интегралом …

2. Площадь фигуры, изображенной на рисунке, 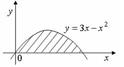 равна …
равна …
- Площадь фигуры, изображенной на заданном рисунке, равна …

- Площадь фигуры, изображенной на рисунке, определяется интегралом …
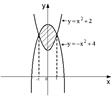
- Найти площадь фигуры, ограниченной линиями у=2х; у=0; х=1; х=3.
- Площадь фигуры, изображенной на заданном рисунке, равна …

 2020-06-08
2020-06-08 87
87








