Возведение в степень произведения, дробей, содержащих корень

 

Применим свойства степеней для выражений, содержащих квадратные корни.

 

Так как (ab)ⁿ=aⁿbⁿ, то .

 или

        

      

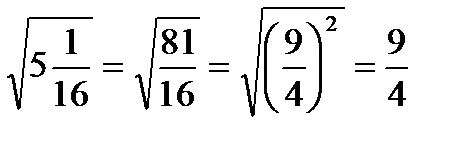
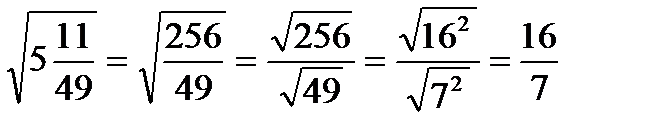
Если подкоренное число нельзя записать в виде квадрата какого-либо числа, значит, его нельзя извлечь из-под корня. В таком случае число либо оставляют под корнем, либо вычисляют значение корня приближённо.

Например, число 5 нельзя представить в виде квадрата. Значит, извлечь нельзя.

, то есть .

Если быть точнее: 2,2< <2,3; ещё точнее 2,23< <2,24 и так далее. Получаем или .

 

 

Решение уравнений, содержащих корень, квадрат

 

Рассмотрим 2 случая : если а≥0 и а<0.

Если а≥0, то по определению арифметического корня . Если a<0, то (-а)>0, поэтому .

Таким образом, для любого числа а справедливо равенство: .

Исходя из этого равенства, можно сформулировать правило решения уравнений вида х²=а.

Для любого уравнения вида х²=а, где а>0, можно записать корни: .

Решением уравнения х²=49 являются два числа: х₁=7 и х₂= –7. Решением же уравнения х²=5 являются два числа: .

Для решения уравнений вида , где а≥0, нужно возвести в квадрат число а.

. Действительно, по определению квадратного корня .

 

 

Тема 12. Иррациональные числа