При переходе от бесконечной периодической десятичной дроби к обыкновенной дроби можно пользоваться следующими правилами: бесконечная десятичная периодическая дробь без допериода равна обыкновенной дроби, числитель которой равен периоду, а знаменатель — числу, записанному столькими девятками, сколько цифр в периоде.
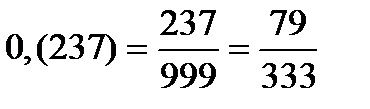
Бесконечная десятичная периодическая дробь с допериодом равна обыкновенной дроби, числитель которой равен разности между числом, записанным цифрами от десятичной запятой до конца первого периода, и числом, записанным цифрами допериода, а знаменатель — числу, записанному столькими девятками, сколько цифр в периоде, и столькими нулями, сколько цифр в допериоде.

Чтобы сравнить числа, записанные в разном виде, нужно сначала представить их в одинаковом виде.
Сравним числа 4,8 и 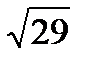 . Представим число 4,8 в виде корня. 4,82=23,04
. Представим число 4,8 в виде корня. 4,82=23,04 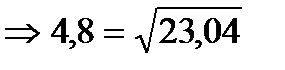 .
. 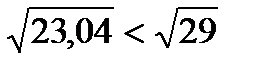 . Значит,
. Значит, 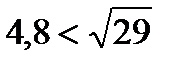 .
.
Тема 14. Функция у= 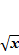 , её свойства и график
, её свойства и график
Область определения функции. Область значения функции. Построение графика функции по точкам. Возрастание и убывание функции. Наибольшее и наименьшее значение функции на определённом промежутке области определения
Для обозначения функции вообще можно использовать любую другую букву латинского (или реже греческого) алфавита: g(x), h(x), s(x), φ(x) и т.д.
В 7 классе мы уже познакомились с линейной функцией y=kx и функцией y=x2 и их графиками. Мы знаем, что графиком функции y=x2, где х≥0, является часть параболы – её правая ветвь. Но и при х≤0 построение параболы возможно. Это говорит о том, что область определения функции у=х2 – вся числовая ось.
Если функция задана формулой и её область определения не указана, то считают, что она совпадает с областью допустимых значений аргумента.
Например, областью определения функции f(x)=х2-2х является множество всех чисел. А областью определения функции 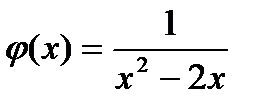 является множество всех чисел, кроме 0 и 2, так как при х=0 и х=2 знаменатель дроби
является множество всех чисел, кроме 0 и 2, так как при х=0 и х=2 знаменатель дроби 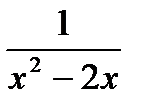 обращается в нуль, а на нуль делить нельзя.
обращается в нуль, а на нуль делить нельзя.
Рассмотрим теперь функцию 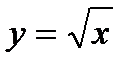 . Так как выражение
. Так как выражение  имеет смысл только при x≥0, значит, область определения (область допустимых значений аргумента) функции
имеет смысл только при x≥0, значит, область определения (область допустимых значений аргумента) функции 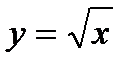 - множество неотрицательных чисел. Другими словами функция
- множество неотрицательных чисел. Другими словами функция 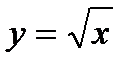 может принимать свои значения только при x≥0.
может принимать свои значения только при x≥0.
Составим таблицу значений функции 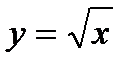 . Значения х берутся произвольно из области определения, а у получаются при подстановке х в уравнение функции.
. Значения х берутся произвольно из области определения, а у получаются при подстановке х в уравнение функции.
| х | 0 | 1 | 4 | 9 | 16 |
| у | 0 | 1 | 2 | 3 | 4 |
Мы получили пары значений, которые являются координатами точек графика функции: А(0;0), В(1;1), С(4;2) и т.д. Построим на координатной плоскости эти точки и плавно соединим. Получится график функции 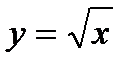 .
.
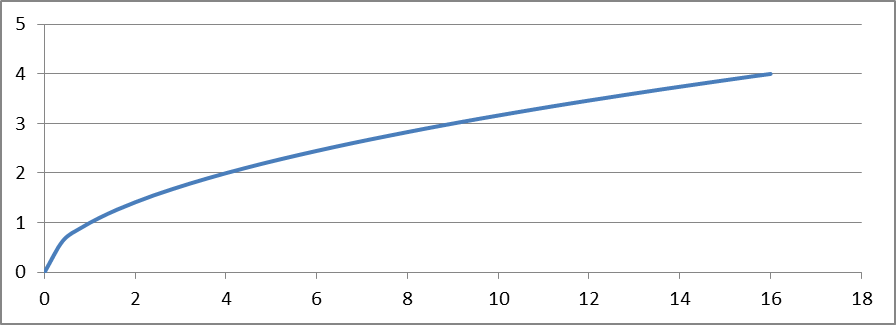
Если взять определённый промежуток области определения функции, то самое большое значение функции на этом промежутке называется её наибольшим значением или максимумом функции, а самое маленькое значение функции на этом промежутке называется её наименьшим значением или минимумом.
На всей области определения функции 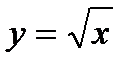 минимальным значением является у=0. Это значение является наименьшим значением функции
минимальным значением является у=0. Это значение является наименьшим значением функции 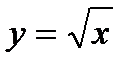 . Но, например, на промежутке [4;9] унаим.=2, а унаиб.=3.
. Но, например, на промежутке [4;9] унаим.=2, а унаиб.=3.
Если при любом x2>x1 значения y2>у1 на каком-либо промежутке области определения, то функция на этом промежутке возрастает. Если же на каком-либо промежутке при x2>x1 значения y2<у1, то функция убывает.
Так как на всем протяжении области определения функции 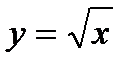 при любом xn+1>xn функция принимает значения yn+1>уn, то функцию можно назвать возрастающей. Она на любом промежутке своей области определения будет возрастать.
при любом xn+1>xn функция принимает значения yn+1>уn, то функцию можно назвать возрастающей. Она на любом промежутке своей области определения будет возрастать.
Нахождение f(a), f(xn), (f(x))n, f(kx), f(x+a)
В любом из случаев f(a), f(xn), f(kx), f(x+a) нужно в выражении f(x) подставить вместо х то значение аргумента, которое указано в скобках, а в случае (f(x))n нужно значение функции f(x) возвести в степень n.
Найдём, например, значения f(a), f(xn), f(kx), f(x+a), (f(x))n для функции 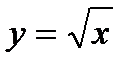 , если a=4, n=6, k=9.
, если a=4, n=6, k=9.
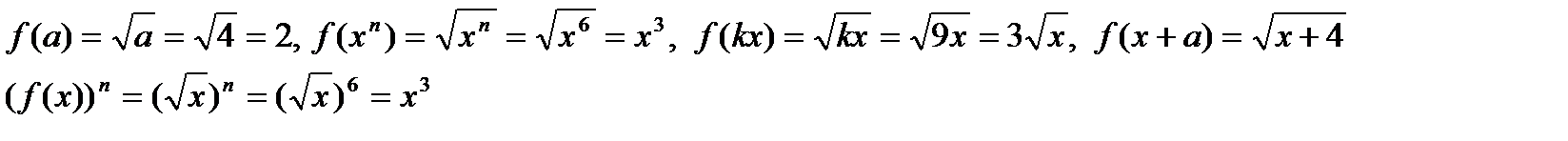
 2020-06-10
2020-06-10 171
171








