2020-06-10
146
Мы уже с вами ранее узнали, что для того чтобы извлечь из-под корня какое-либо число, необходимо представить его в виде квадрата. А результат извлечённого из-под корня числа выражается при этом рациональным числом. Если же подкоренное выражение нельзя представить в виде квадрата, а результат извлечения из-под корня не является числом рациональным, то такое число называется иррациональным. Иррациональные числа обозначаются I.
Так, например, число 2 не является рациональным. Его десятичное представление является бесконечной непериодической дробью: 2 = 1,414213562373095048801688724209….
Числа, которые представляются бесконечными непериодическими десятичными дробями, являются иррациональными.
Для сравнения иррациональных чисел, а также для решения некоторого типа задач часто приходится внести выражение под знак корня или вынести из-под него. Для этого пользуются определением квадратного корня и правилом извлечения корней из произведения и дроби.
и наоборот 
Сравним 
и 
. Представим число в виде корня, а затем сравним полученные выражения. 
. 
. Значит, < .
Свойства квадратных корней
Систематизируем все свойства квадратных корней, которые мы рассмотрели.
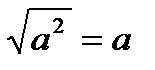, где а≥0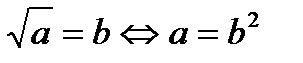 
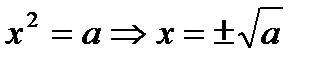
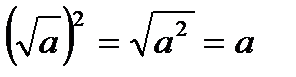
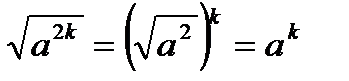
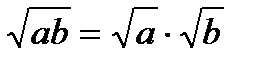
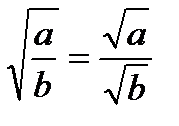
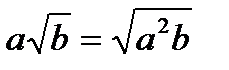если a>b, то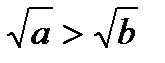 
Тема 13. Множество действительных чисел
Обозначение действительных чисел. Состав множества R. Сравнение десятичных дробей, чисел с разными знаками
Рациональные и иррациональные числа вместе составляют множество действительных чисел. Множество действительных чисел обозначают R.
Взаимосвязь всех числовых множеств можно показать на рисунке.
| Q I |
| N |
| Z |
| R |
Сравним числа 0,45678… и −1,23459…. Поскольку первое из данных чисел положительное, а второе отрицательное, то 0,45678… > −1,23459…
Сравним числа 3,14159… и 3,14295…. У этих бесконечных десятичных дробей одинаковые целые части, десятые и сотые, но разряд тысячных первого числа содержит 1 единицу, а второго — 2 единицы. Поэтому 3,14159… < 3,14295…
