Решение простейших неравенств вида x≥a, x≤a, x>a, x<a. Запись решений в виде промежутков
Неравенство с переменной выделяет из множества всех чисел определенную его часть. Рассмотрим двойное неравенство −3 < c < 4. Отметим на координатной прямой точки A и B с координатами −3 и 4. Точка X(c), координата которой удовлетворяет неравенству −3 < c < 4, лежит между точками A (−3) и B (4), и наоборот, если точка X(c) лежит между точками A (−3) и B (4), то её координата c удовлетворяет неравенству −3 < c < 4.
| А Х В – 3 с 4 |
Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство.
Решить неравенство – значит найти множество его решений, иначе говоря, решить неравенство – значит найти все его решения или доказать, что их нет.
Неравенства, множества решений которых совпадают, называются равносильными.
В частности, неравенства, не имеющие решений, являются равносильными.
При решении неравенств стремятся данное неравенство заменить более простым, равносильным ему, для которого множество решений легко указать.
Для того чтобы сформулировать условия перехода к равносильному неравенству, введём понятие области определения неравенства.
Областью определения неравенства с одной переменной называется множество значений переменной, при которых обе части неравенства имеют смысл.
Например, областью определения неравенства 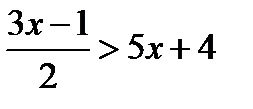 является множество всех чисел (то есть решением данного неравенства возможно любое число), а неравенства
является множество всех чисел (то есть решением данного неравенства возможно любое число), а неравенства 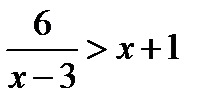 – множество, состоящее из всех чисел, кроме 3.
– множество, состоящее из всех чисел, кроме 3.
Рассмотрим примеры решения простейших неравенств.
Пример. Решим неравенство 0,2х>4.
Разделим обе части неравенства на 0,2. Получим: x>20. Это и есть решение неравенства 0,2х>4. Ответ можно записать как в виде неравенства (x>20), так и в виде промежутка:  .
.
Пример 2. Решим неравенство  .
.
Разделим обе части неравенства на отрицательное число –18, изменив при этом знак неравенства на противоположный. Получим:  . Множество решений неравенства – числовой промежуток
. Множество решений неравенства – числовой промежуток  .
.
Итак, рассмотрим решения всех простейших неравенств.
| Вид неравенства |
| Запись решения в виде промежутка | Название промежутка | |
| x>a |
| 
| Открытый числовой луч | |
| x≥a |
| 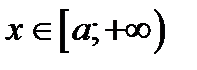
| Числовой луч | |
| x<a |
| 
| Открытый числовой луч | |
| x≤a | 
| Числовой луч |
Алгоритм решения линейных неравенств ax+b≤kx+m и т.п.
Каждое из неравенств ax < b; ax > b; ax ≥ b; ax ≤ b, где x — переменная, а a и b — некоторые числа, называется линейным неравенством с одной переменной.
При решении неравенств используются такие свойства:
1. Любой член неравенства можно переносить из одной части неравенства в другую, изменив знак этого члена на противоположный; при этом знак неравенства не меняется.
2. Обе части неравенства можно умножить или разделить на одно и то же число, не равное нулю; если это число положительно, то знак неравенства не меняется, а если это число отрицательно, то знак неравенства меняется на противоположный.
Эти свойства позволяют заменять данное неравенство другим, имеющим те же решения. Для решения неравенства с одним неизвестным, которое сводится к линейному, нужно:
1) произвести необходимые преобразования неравенства (прибавить или вычесть какое либо число, умножить или разделить на нужное положительное число)
2) перенести члены, содержащие неизвестное, в левую часть, а члены, не содержащие неизвестное, в правую;
3) приведя подобные члены, разделить обе части неравенства на коэффициент при неизвестном, если он не равен нулю.
При решении линейных неравенств возможны двойные неравенства. Рассмотрим все виды числовых промежутков, которые могут понадобиться для записи ответа.
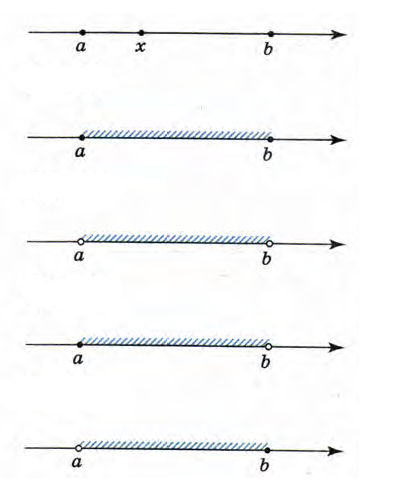 Пусть а и b – некоторые числа, причём a<b. Отметим на координатной прямой точки с координатами а и b. Если точка расположена между ними, то ей соответствует число х, которое больше а и меньше b. Верно и обратное: если число х больше а и меньше b, то оно изображается точкой, лежащей между точками с координатами а и b.
Пусть а и b – некоторые числа, причём a<b. Отметим на координатной прямой точки с координатами а и b. Если точка расположена между ними, то ей соответствует число х, которое больше а и меньше b. Верно и обратное: если число х больше а и меньше b, то оно изображается точкой, лежащей между точками с координатами а и b.
 числовой отрезок
числовой отрезок
 интервал
интервал
 полуинтервал
полуинтервал
 полуинтервал
полуинтервал
Пример 1. Решим для примера неравенство. 
Умножим обе части неравенства на 6: 

Раскроем скобки и приведём подобные члены: 
 откуда
откуда  или
или  .
.
Пример 2. Решим неравенство 6(d − 3) + 5 d > 12(d − 1) − d.
Раскроем скобки и выполним перенесение слагаемых:
6 d − 18 + 5 d > 12 d − 12 − d;
6 d + 5 d − 12 d + d > −12 + 18.
После приведения подобных получаем: 0 · d > 6.
Это неравенство не имеет решений, поскольку оно при любом значении переменной d преобразуется в числовое неравенство 0 > 6, которое ложно. Поэтому не имеет решений и данное неравенство, поскольку оно равносильно неравенству 0 · d > 6.
Ответ. Неравенство не имеет решений.
Пример 3. Решим неравенство 7(3 + k) ≥ 3(k + 5) + 4 k − 13.
Имеем: 21 + 7 k ≥ 3 k + 15 + 4 k − 13; 7 k − 3 k − 4 k ≥ 15 − 13 − 21; 0 · k ≥ −19.
При любом значении переменной k неравенство 0 · k ≥ −19 преобразуется в числовое неравенство 0 ≥ −19, которое истинно. Поэтому его решением является любое число. Это означает, что и исходное неравенство своим решением имеет любое число.
Ответ. Решение неравенства — любое число.
Иногда приходится решать линейные неравенства, имеющие общие решения. Такие неравенства мы встречаем при решении систем неравенств.
При решении систем возникает необходимость в объединении или пересечении промежутков.
Объединение промежутков.

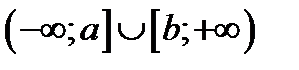

Пересечение промежутков.


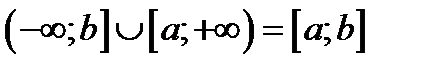
Решим для примера одну систему неравенств.
 Последовательно получаем:
Последовательно получаем: 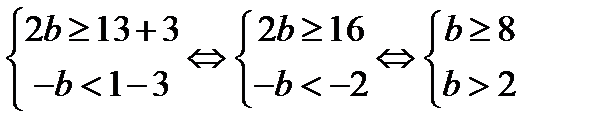
Множество решений каждого из неравенств b≥8 и b>2 изобразим на координатной прямой.
То, что неравенства объединены в систему,
говорит о том, что её решением будет пересечение множеств решений каждого неравенства.
Ответ: 
 2020-06-10
2020-06-10 165
165








