Второй способ решения квадратных неравенств – метод интервалов. Он плавно вытекает из предыдущего способа. В методе интервалов первое – это определить точки, в которых квадратный трёхчлен равен нулю. А это не что иное, как точки пересечения параболы с осью О х. Для этого определения нет необходимости каждый раз полностью чертить график функции. Достаточно разложить квадратный трёхчлен на множители, нарисовать ось Ох, отметить на ней нули функции, нарисовать схематически часть параболы, обращая внимание на направление ветвей, расставить знаки и выделить ту часть графика, который соответствует знаку неравенства.
Поясним этот метод на примере.
Решим неравенства 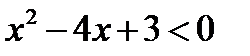 и
и 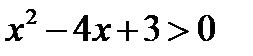 . Для решения обоих неравенств достаточно один раз пройти весь алгоритм, а в последнем пункте для каждого из неравенств выбрать нужно решение.
. Для решения обоих неравенств достаточно один раз пройти весь алгоритм, а в последнем пункте для каждого из неравенств выбрать нужно решение.
1) Разложим на множители 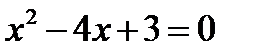 , а для этого найдём корни уравнения. х1=1, х2=3. Получаем:
, а для этого найдём корни уравнения. х1=1, х2=3. Получаем: 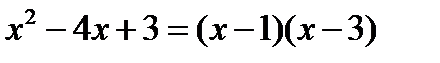 .
.
2) Точки х =1 и х =3 разбивают числовую ось на 3 промежутка: 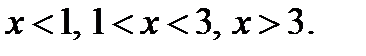
Отмечаем на числовой оси корни уравнения 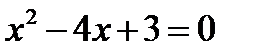 . Ветви параболы, определённой этим уравнением направлены вверх. Нарисуем схематически параболу на этой оси.
. Ветви параболы, определённой этим уравнением направлены вверх. Нарисуем схематически параболу на этой оси.
|
|
|
х
1 3
Заметим, что левее 1 и правее 3 парабола выше оси, а значит, на этих промежутках значения у>0, а в промежутке между 1 и 3 значения у<0.
Теперь соответствующие значения у выберем для записи решения неравенств.
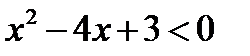 при
при 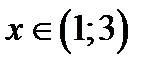 , а
, а 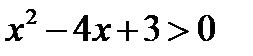 при
при 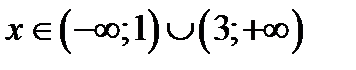 .
.
Интересно заметить, что с помощью этого же рисунка можно решить неравенства
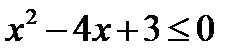 и
и 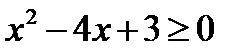 . В этом случае нам достаточно только поменять вид скобок с круглых на квадратные там, где стоят числа 1 и 3.
. В этом случае нам достаточно только поменять вид скобок с круглых на квадратные там, где стоят числа 1 и 3.
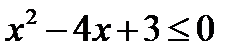 при
при 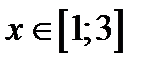 , а
, а 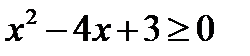 при
при 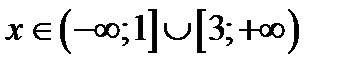 .
.
Метод интервалов применим не только к квадратному трёхчлену в стандартном виде. Если неравенство в левой части уже представляет собой произведение вида (х – х1)(х – х2), причём множители могут стоять в какой-либо степени, то можно сразу отметить на числовой оси точки х1 и х2. Если все степени множителей нечётные, а произведение имеет перед переменной х всегда положительный знак, то первым знаком справа всегда будет «+», остальные знаки чередуются. Если какой либо множитель стоит в чётной степени, то этот хn можно не включать в перечень корней, так как он не меняет знака промежутка. Если же в каком-либо множителе х стоит со знаком «-», то знаки расставляют уже по-другому. Чтобы не сбиться в правильности расстановки знаков промежутков, нужно привести левую часть неравенства к виду (х – х1)(х – х2), где перед х стоят «плюсы». Преобразовывать мы уже умеем, зная, что при делении на отрицательное число знак неравенства меняется.
|
|
|
Для иллюстрации сказанного приведём примеры.
+ - +
(х – 5)(х + 4) > 0
– 4 5
Ответ: 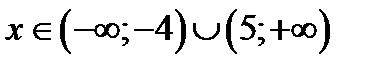
(5 – х)(х + 4) < 0 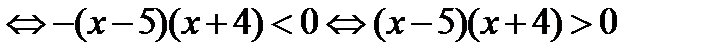 То есть решение (5– х)(х+ 4)<0 будет таким же.
То есть решение (5– х)(х+ 4)<0 будет таким же.
Решим теперь такое неравенство (х – 5)2(х + 4) > 0
(х – 5)2>0 при любом х, поэтому решение будет идентичным решению неравенства (х+4)>0 или x> – 4 и выглядеть так:
– + +
– 4 5
Решим ещё одно неравенство: 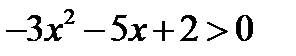 .
.
Чтобы удобнее проводить вычисления, представим данное неравенство в виде квадратного неравенства с положительным первым коэффициентом. Для этого умножим обе его части на – 1: 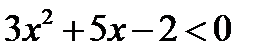 .
.
Представим наше неравенство в виде 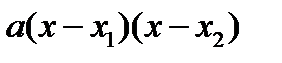 . Найдём корни уравнения
. Найдём корни уравнения 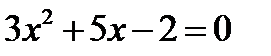 .
. 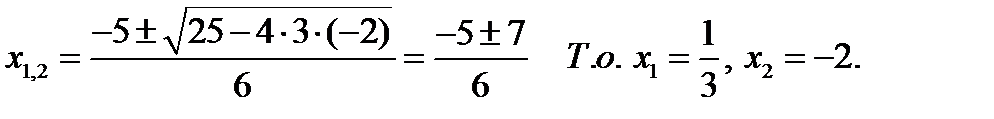
Получим: 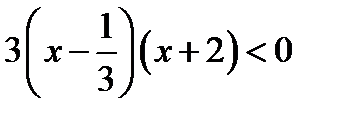 .
.
+ – +
– 2 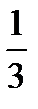
 2020-06-10
2020-06-10 146
146








