ЗАНЯТИЕ № 8
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
ЧАСТЬ А)
РОТОР ВЕКТОРНОГО ПОЛЯ. ФОРМУЛА СТОКСА
Ротор векторного поля
Ротором векторного поля 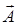 называется векторная функция, которую в декартовых координатах определяют формулой
называется векторная функция, которую в декартовых координатах определяют формулой 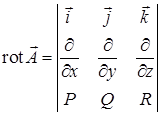 .
.
В результате разложения определителя по первой строке получим
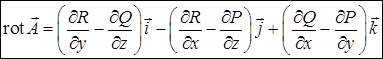 .
.
Ротор является дифференциальным оператором первого порядка. Он обладает свойством линейности: 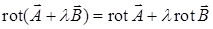 , где
, где 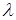 — числовая константа.
— числовая константа.
Отметим, что в криволинейных координатах (например, в цилиндрических или сферических) формула для вычисления ротора имеет другой вид.
Циркуляция векторного поля. Формула Стокса
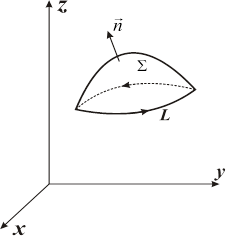 |
| Рис. 16.1 |
Циркуляцией векторного поля 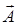 называется криволинейный интеграл 2-го рода
называется криволинейный интеграл 2-го рода 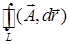 по замкнутому контуру
по замкнутому контуру 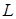 . Если поле
. Если поле 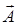 является непрерывно дифференцируемым, а контур
является непрерывно дифференцируемым, а контур 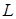 – кусочно-гладким, то циркуляция равна потоку ротора этого векторного поля через произвольную кусочно-гладкую поверхность
– кусочно-гладким, то циркуляция равна потоку ротора этого векторного поля через произвольную кусочно-гладкую поверхность 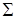 , ограниченную контуром
, ограниченную контуром 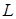 :
:
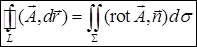 (формула Стокса).
(формула Стокса).
Направление обхода контура и выбор стороны поверхности согласованы следующим образом: если смотреть из конца нормали 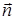 , то обход контура
, то обход контура 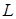 осуществляется против часовой стрелки (рис. 16.1). При изменении направления обхода контура циркуляция меняет знак.
осуществляется против часовой стрелки (рис. 16.1). При изменении направления обхода контура циркуляция меняет знак.
Формула Стокса является обобщением формулы Грина (см. п. 14.3) на пространственный случай.
В координатной записи она имеет вид
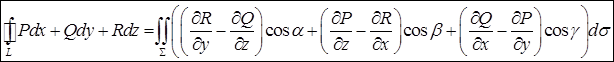 .
.
Здесь 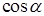 ,
, 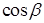 ,
, 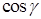 – координаты единичной нормали
– координаты единичной нормали 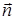 к поверхности
к поверхности 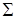 , опирающейся на контур
, опирающейся на контур 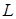 , а
, а 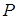 ,
, 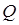 и
и 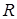 – компоненты векторного поля
– компоненты векторного поля 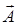 .
.
Решение некоторых типовых задач, рассматриваемых в аудитории
16.3.1. Вычислить ротор векторного поля 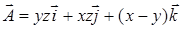 .
.
Решение. Здесь 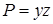 ,
, 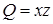 и
и 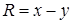 . Компоненты ротора равны
. Компоненты ротора равны 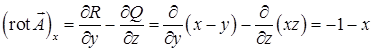 ,
, 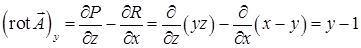 ,
,
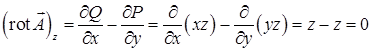 .
.
Итак, 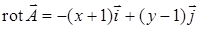 .
.
16.3.2. Найти по формуле Стокса циркуляцию векторного поля 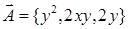 по окружности
по окружности 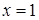 ,
, 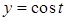 ,
, 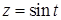 , ориентированной против часовой стрелки при взгляде на нее из начала координат.
, ориентированной против часовой стрелки при взгляде на нее из начала координат.
Решение. Выберем в качестве поверхности 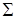 , ограниченной данной окружностью
, ограниченной данной окружностью 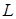 , круг
, круг 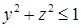 при
при 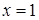 . Поскольку контур обходится против часовой стрелки при взгляде из начала координат, согласованной единичной нормалью к поверхности
. Поскольку контур обходится против часовой стрелки при взгляде из начала координат, согласованной единичной нормалью к поверхности 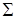 является вектор
является вектор 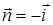 . Найдем ротор векторного поля:
. Найдем ротор векторного поля: 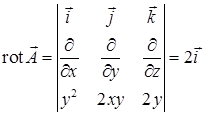 , тогда
, тогда 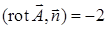 . По формуле Стокса
. По формуле Стокса 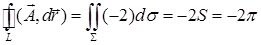 , где
, где 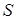 – площадь круга
– площадь круга 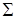 , радиус которого равен единице.
, радиус которого равен единице.
16.3.3. Вычислить циркуляцию вектора 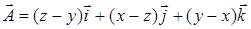 вдоль контура
вдоль контура 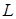 :
: 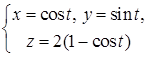 в направлении, соответствующем возрастанию параметра
в направлении, соответствующем возрастанию параметра 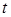 . Задачу решить по формуле Стокса и прямым вычислением.
. Задачу решить по формуле Стокса и прямым вычислением.
Решение. Как видно из параметрического задания кривой, 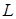 — это эллипс, являющийся пересечением цилиндра
— это эллипс, являющийся пересечением цилиндра 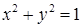 и плоскости
и плоскости 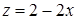 . В качестве поверхности
. В качестве поверхности 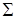 , опирающейся на контур
, опирающейся на контур 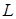 , возьмем часть этой плоскости, ограниченную данным эллипсом. Если смотреть из начала координат, при возрастании
, возьмем часть этой плоскости, ограниченную данным эллипсом. Если смотреть из начала координат, при возрастании 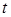 контур обходится по часовой стрелке, поэтому нормалью к
контур обходится по часовой стрелке, поэтому нормалью к 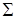 , согласованной с направлением обхода контура, будет единичный нормальный вектор плоскости
, согласованной с направлением обхода контура, будет единичный нормальный вектор плоскости 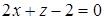 с положительной аппликатой, т. е.
с положительной аппликатой, т. е. 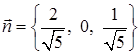 .
.
Теперь найдем ротор:
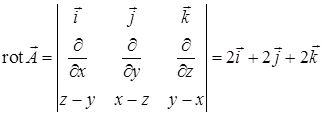 . Скалярное произведение
. Скалярное произведение 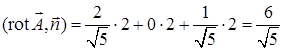 . По формуле Стокса циркуляция равна
. По формуле Стокса циркуляция равна 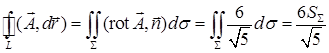 . Проекцией эллипса на плоскость
. Проекцией эллипса на плоскость 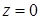 является окружность
является окружность 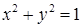 , ограничивающая круг, площадь которого равна
, ограничивающая круг, площадь которого равна 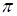 . Косинус угла между плоскостями
. Косинус угла между плоскостями 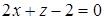 и
и 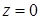 равен
равен 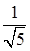 , тогда по формуле площади проекции
, тогда по формуле площади проекции 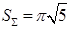
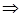
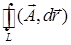
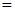
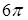 .
.
Вычислим теперь циркуляцию непосредственно, используя параметрическое задание контура: 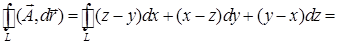
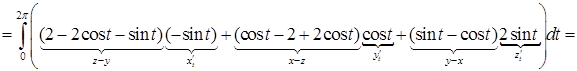
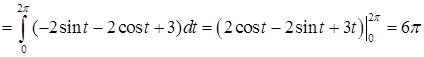 .
.
16.3.4. Найти циркуляцию вектора 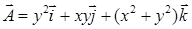 вдоль контура
вдоль контура 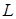 , вырезанного на параболоиде
, вырезанного на параболоиде 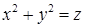 плоскостями
плоскостями 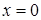 ,
, 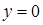 ,
, 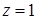 при
при 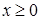 ,
, 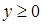 . Контур
. Контур 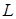 обходится по часовой стрелке при взгляде со стороны положительных значений координаты
обходится по часовой стрелке при взгляде со стороны положительных значений координаты 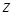 .
.
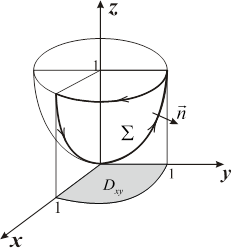 |
| Рис. 16.2 |
Решение. Контур состоит из двух дуг парабол и четверти окружности (рис. 16.2). Направление обхода контура, указанное в условии, соответствует выбору внешней нормали 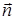 к параболоиду, т. е. нормали с отрицательной аппликатой. В качестве поверхности
к параболоиду, т. е. нормали с отрицательной аппликатой. В качестве поверхности 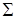 , ограниченной контуром
, ограниченной контуром 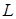 , выберем часть параболоида.
, выберем часть параболоида.
По формуле Стокса 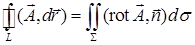
Вычислим ротор
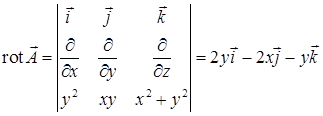 . Чтобы найти поток ротора, выберем метод проектирования на одну координатную плоскость, изложенный в п. 13.1, а именно, на плоскость
. Чтобы найти поток ротора, выберем метод проектирования на одну координатную плоскость, изложенный в п. 13.1, а именно, на плоскость 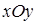 . Проекцией поверхности
. Проекцией поверхности 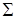 является четверть круга
является четверть круга 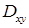 радиуса
радиуса 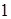 . Уравнение поверхности
. Уравнение поверхности 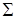 :
: 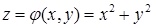 , компоненты ротора
, компоненты ротора 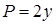 ,
, 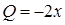 ,
, 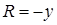 . Учтем, что, в отличие от п. 13.1, мы выбрали нормаль к
. Учтем, что, в отличие от п. 13.1, мы выбрали нормаль к 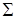 , составляющую тупой, а не острый угол с осью
, составляющую тупой, а не острый угол с осью 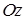 , поэтому
, поэтому
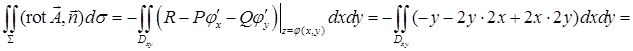
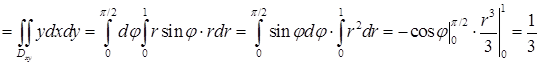 .
.
Итак, циркуляция равна 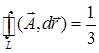 .
.
16.3.5. Найти циркуляцию векторного поля 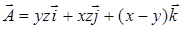 вдоль эллипса, образованного пересечением эллипсоида
вдоль эллипса, образованного пересечением эллипсоида 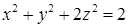 с плоскостью
с плоскостью 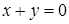 .
.
Решение. Ротор этого поля найден в примере 16.3.1. В качестве поверхности, опирающейся на контур, выберем участок плоскости 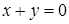 внутри эллипсоида
внутри эллипсоида 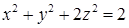 . Единичная нормаль к плоскости
. Единичная нормаль к плоскости 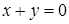 равна
равна 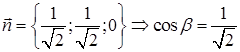 ,
, 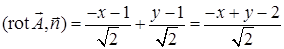 . На выбранной поверхности
. На выбранной поверхности 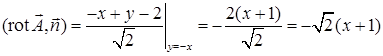 . Исключим из уравнений эллипсоида и плоскости
. Исключим из уравнений эллипсоида и плоскости 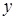 :
: 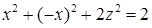 , или
, или 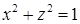 . Следовательно, проекция поверхности интегрирования
. Следовательно, проекция поверхности интегрирования 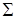 на плоскость
на плоскость 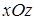 есть круг радиуса 1. По формуле Стокса получаем:
есть круг радиуса 1. По формуле Стокса получаем:
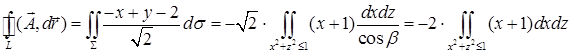 . Двойной интеграл вычислим в полярных координатах:
. Двойной интеграл вычислим в полярных координатах:
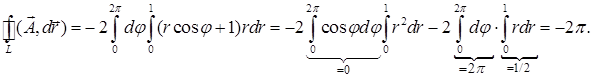
 2020-06-29
2020-06-29 3094
3094