2020-06-29
91
Пусть даны два комплексных числа в тригонометрической форме 
, тогда 
,
т.е. 
, 
. Получили формулу: 
. При умножении комплексных чисел, заданных в тригонометрической форме, модули перемножаются, а аргументы складываются.
Полученная формула справедлива и для произведения 
комплексных чисел. При этом имеем 
. Полагая в равенстве 
, найдем: 
, т.е. 
; 
. Эта формула называется формулой Муавра.
Деление. Рассмотрим деление двух комплексных чисел, заданных в тригонометрической форме 
.
.
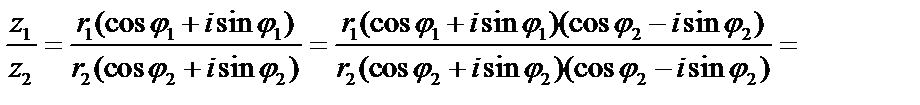
Следовательно, 
, т.е. 
.
При делении комплексных чисел, заданных в тригонометрической форме, модуль частного равен частному их модулей, а из аргумента делимого вычитаем аргумент делителя.
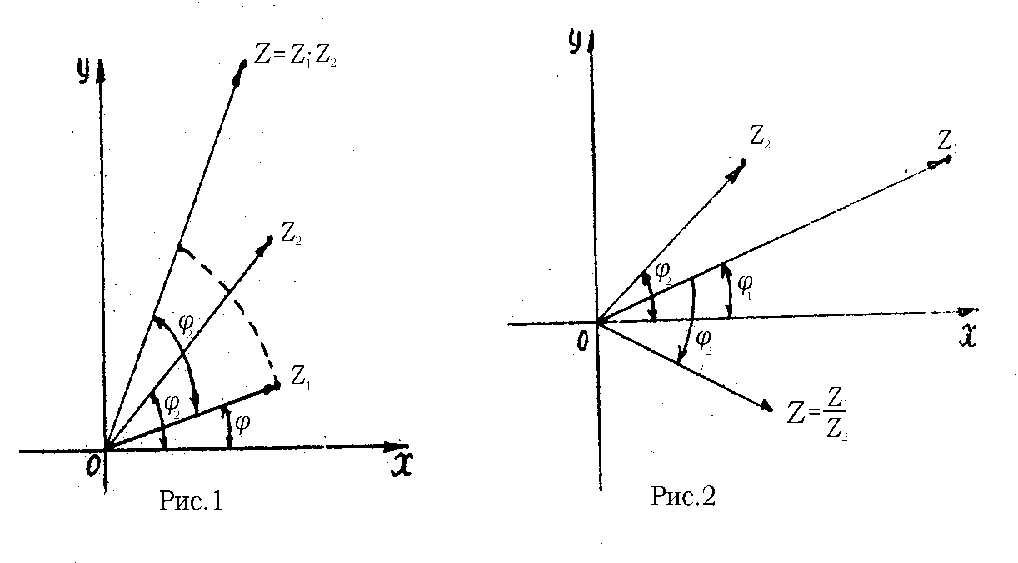
Дадим геометрическую интерпретацию умножения и деления комплексных чисел. Из формулы умножения следует, что при умножении комплексных чисел 
на 
вектор OZ, поворачивается около начала 0 (0,0) против часовой стрелки на угол 
и сжимается (растягивается) в 
раз, если 
(рис.1).
При делении же комплексных чисел на , согласно формуле, вектор OZ, поворачивается около точки 0 (0,0) по часовой стрелке на угол и сжимается (растягивается) в раз, если (рис.2).
Извлечение корня. Пусть дано комплексное число 
. Надо найти комплексное число 
., удовлетворяющее условию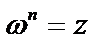 
. Согласно формуле Муавра, получим: 
.
Отсюда находим 
или 
Таким образом, имеем 
,где 
.
Первые равенства показывают, что модули всех корней 
одинаковы и расположены на окружности радиуса 
с центром в начале координат. Обозначим одно из значений корня с аргументом 
, полученное из формулы при k = 0 через 
; тогда 
Полагая затем 
, найдем следующее значение корня 
с аргументом 
: 
; его можно получить из первого значения поворота на угол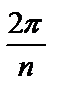 
. Затем, полагая 
, находим все значения корня. Каждое последующее получается из предыдущего поворотом на один и тот же угол .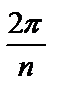
Следовательно, все n значений корней 
делят окружность радиуса 
на n равных частей, т.е. являются вершинами правильного n – угольника, вписанного в эту окружность.
Пример 4. Вычислить 
Решение. Получим тригонометрическую форму комплексного числа: 
.Применяя формулу Муавра для 
, получаем:
.
Пример 5. Вычислить 
.
Решение. Представим число 1 в тригонометрической форме. Имеем 
,тогда по формулам, получим: 
, т.е. число находится на положительной полуоси ОХ. Из формулы находим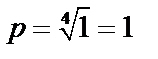 
, значит, все значения корней лежат на единичной окружности 
. Далее 
и 
. Все значения 
лежат в вершинах квадрата, вписанного в единичную окружность , причем одна из вершин этого квадрата – точка (1,0), а остальные значения корней 
можно получить поворотом на угол 
первого значения корня 
, 
;
; 
;
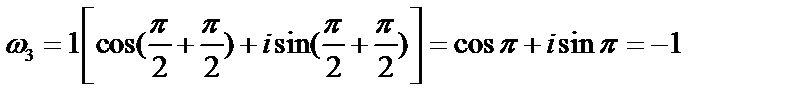Пример 6. Найти все значения 
.
Решение. Представим число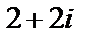 
в тригонометрической форме. Это число лежит в первой четверти; по формулам находим 
.
Следовательно, 
По формулам определяем корни: 
,
отсюда получим:
при 
,
.
12.3. Понятие дифференциального уравнения. Задача Коши
Дифференциальное уравнение – уравнение, связывающее аргумент x,исходную функцию y и её производные. Порядок старшей производной называется порядок дифференциального уравнения.
Всякая 
– решение, если она обращает его в тождество.
Общее решение дифференциального уравнения n –го порядка содержит n констант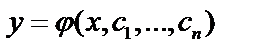 
, иногда получаем ответ в виде: 
это общий интеграл.
Дифференциальное уравнение I-го порядка
Это дифференциальное уравнение вида 
, иногда 
.
Общее решение 
, с – произвольная постоянная.
Геометрически общее решение – семейство интегральных кривых.
Если задать точку 
, через которую проходить кривая, то тем самым из бесконечного числа кривых выделяется 1 кривая – частное решение.
Аналитически – имеется начальное условие: 
из общего решения находится частное. Это задача Коши.
Пример. Решить задачу Коши: 
– частное решение.
Дифференциальное уравнение первого порядка можно записать 
или 
.
Рассмотрим решение некоторых дифференциальных уравнений первого порядка.
