Если искомая функция 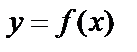 есть функция одного независимого переменного, то дифференциальное уравнение называют обыкновенным.
есть функция одного независимого переменного, то дифференциальное уравнение называют обыкновенным.
Дифференциальное уравнение порядка
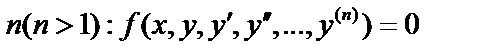 . Всякая функция
. Всякая функция 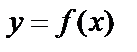 определённая
определённая
и 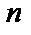 раз дифференцируемая, называется решением этого уравнения, если она обращает его в тождество.
раз дифференцируемая, называется решением этого уравнения, если она обращает его в тождество.
Решение 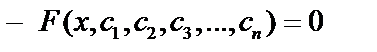 . Задача Коши: найти такое решение д.у., чтобы оно само и его производные до порядка
. Задача Коши: найти такое решение д.у., чтобы оно само и его производные до порядка 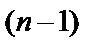 при
при 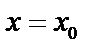 принимали бы заданные значения
принимали бы заданные значения 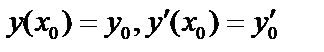 ,
, 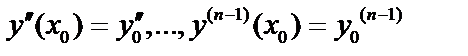 где
где 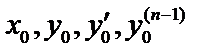 заданные числа, называемые начальными условиями. Задача Коши – значение функции и производных задаются при одном и том же значении
заданные числа, называемые начальными условиями. Задача Коши – значение функции и производных задаются при одном и том же значении 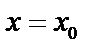 .
.
Общее решение: если задачу Коши можно решить при любых начальных значениях, то 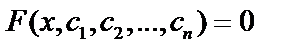 – общее решение.
– общее решение.
Понижение порядка
I. 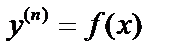 . Общее решение – интегрирование
. Общее решение – интегрирование 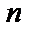 раз:
раз:  .
.
Пример: 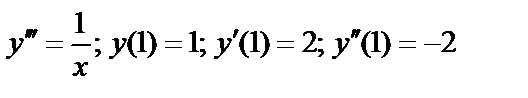 .
.
 ,
,
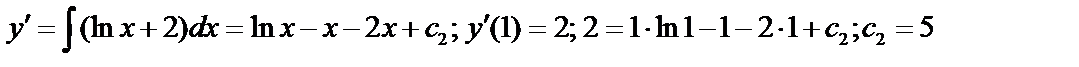

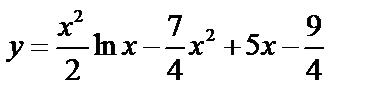 .
.
II. Уравнения, не содержащие искомой функции 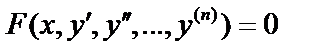 . Порядок может быть понижен на 1:
. Порядок может быть понижен на 1: 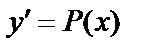 получим уравнение
получим уравнение 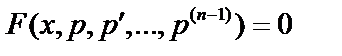 . Если уравнение не содержит искомой функции y или её производных до порядка
. Если уравнение не содержит искомой функции y или её производных до порядка 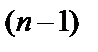 , т.е.
, т.е. 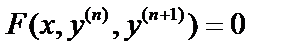 , то порядок может быть понижен на
, то порядок может быть понижен на 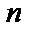 единиц:
единиц: 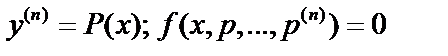 .
.
Пример: 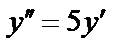 ; подстановка
; подстановка 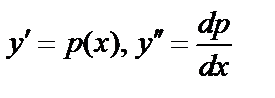 ; тогда
; тогда 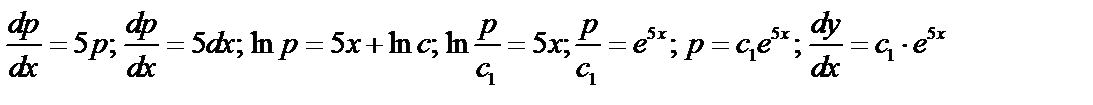 ;
;
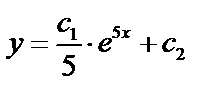 .
.
III. Уравнения, не содержащие независимой переменной 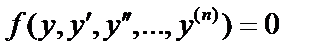 . Понижение порядка на
. Понижение порядка на 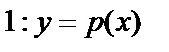

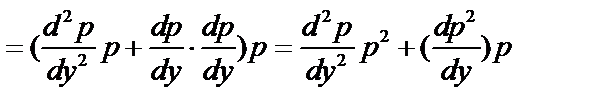
Общее решение уравнения: 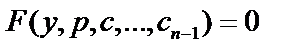 ;
;  - I -го порядка.
- I -го порядка.
Пример: 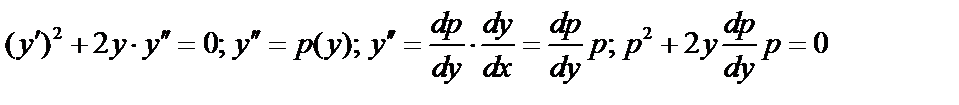
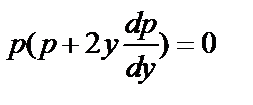 ,
,
а) 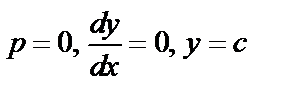 ;
;
б) 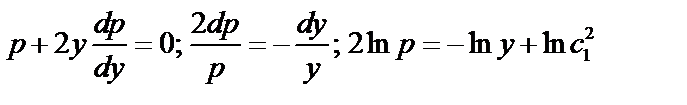 ;
;
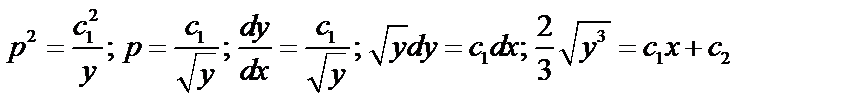 ;
;
 .
.
 2020-06-29
2020-06-29 93
93








