Пусть имеем уравнение:  где
где  и
и  – действительные числа. Пусть правая часть имеет вид:
– действительные числа. Пусть правая часть имеет вид:  где
где  и
и  вещественные числа,
вещественные числа,  и
и  – многочлены одной или разных степеней. Если они разной степени, то пусть n – их наибольшая степень. Решение можно определить методом вариации произвольных постоянных, однако можно отыскать решение более простым методом неопределённых коэффициентов.
– многочлены одной или разных степеней. Если они разной степени, то пусть n – их наибольшая степень. Решение можно определить методом вариации произвольных постоянных, однако можно отыскать решение более простым методом неопределённых коэффициентов.
Рассмотрим два случая:
1. число  не является корнем характеристического уравнения соответствующего однородного д.у. В этом случае частное решение ищем в виде: (1)
не является корнем характеристического уравнения соответствующего однородного д.у. В этом случае частное решение ищем в виде: (1)  , где
, где  и
и  – многочлены одной и той же степени, равной наивысшей степени
– многочлены одной и той же степени, равной наивысшей степени  и
и  . Необходимо определить коэффициенты многочленов
. Необходимо определить коэффициенты многочленов  и
и  .
.
2. Если число  является корнем кратности
является корнем кратности  характеристического уравнения, то частное решение ищем в виде:
характеристического уравнения, то частное решение ищем в виде:
(2)  . Ищем коэффициенты
. Ищем коэффициенты  и
и  .
.
В обоих случаях определяем коэффициенты многочленов так: в данное уравнение подставляем  и сравниваем коэффициенты при одинаковых степенях x в левой и правой частях равенства. Получаем систему уравнений, из которых определяем коэффициенты многочленов
и сравниваем коэффициенты при одинаковых степенях x в левой и правой частях равенства. Получаем систему уравнений, из которых определяем коэффициенты многочленов  и
и  .
.
Пример 1:
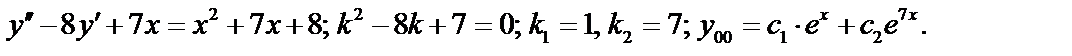 В правой части отсутствует множитель
В правой части отсутствует множитель  , следовательно,
, следовательно,  и правая часть не содержит
и правая часть не содержит 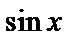 и
и  , это значит, что
, это значит, что  . Число
. Число  не является корнем характеристического уравнения. Частное решение ищем в виде (1), где
не является корнем характеристического уравнения. Частное решение ищем в виде (1), где  , степень многочлена
, степень многочлена  – вторая
– вторая  .
.
 . Найти A,B,C.
. Найти A,B,C.  Подставим в уравнение:
Подставим в уравнение:
 ;
;
 .
.


 .
.
Пример 2:  ;
;
 ,
,
 не корень, характеристическое уравнение, поэтому
не корень, характеристическое уравнение, поэтому 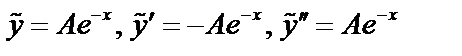 .
.
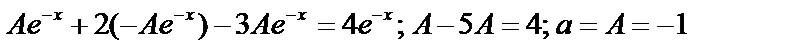 .
.
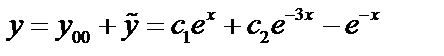 .
.
Пример 3:  - не корень.
- не корень.


 ,
,

 .
.
Пример 4:
 ;
;
 - решение характеристического уравнения.
- решение характеристического уравнения.
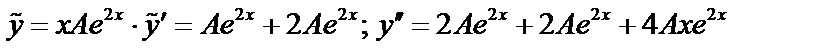 ;
;
 .
.

 2020-06-29
2020-06-29 112
112








