План
1.Поняття екстремуму функції.
2.Необхідні умови екстремуму.
3.Достатні умови екстремуму.
4.Побудова лінійної і квадратичної залежності між двома змінними величинами, за допомогою способу найменших квадратів.
5.Умовний екстремум функцій багатьох змінних.
6. Знаходження найбільшого та найменшого значень функції в замкненій області.
| 1 |
Точка М0(х0) є точкою локального максимуму (мінімуму) функції u = f(x), якщо існує такий окіл точки М0 О(М0), М=М виконується умова
f(M)< f(M0) (f(M) > f (M0)).
| 2 |
34
Необхідні умови екстремуму. Якщо диференційовна функція u = f(x) в точці М0 має локальний екстремум, то
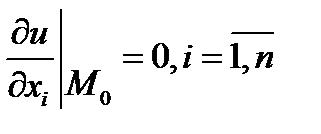
або
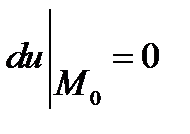
Точки, в яких виконується умова (6.1), називається стаціонарними.
Приклад. Знайти критичні точки функції
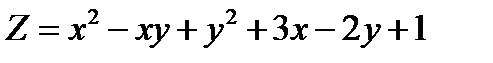
Розв`язання. Спочатку знайдемо частинні похідні першого порядку заданої функції двох змінних:
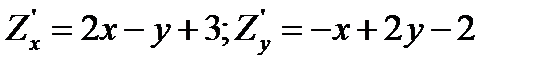
Ці похідні існують для усіх x та y тому критичними будуть лише точки де частинні похідні дорівнюють нулю, тобто
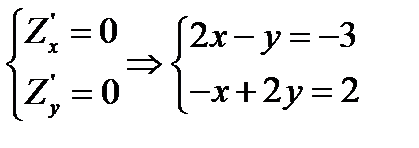
Остання система –лінійна,неоднорідна,з двома невідомими Розв`язуючи, систему за правилом Крамера,одержимо:

| 3 |
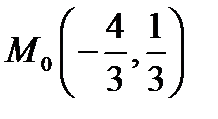 .
.
Достатні умови екстремуму.
Нехай функція u = f(x) двічі диференційована в точці М0 та деякому її околі і точка М0 – стаціонарна точка цієї функції. Тоді
1)якщо 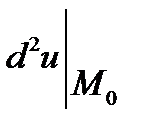 диференціал є знаковизначеною квадратичною формою незалежних змінних dx1, dx2,.dxn, то функція u = f(x) має в цій точці екстремум, причому
диференціал є знаковизначеною квадратичною формою незалежних змінних dx1, dx2,.dxn, то функція u = f(x) має в цій точці екстремум, причому
а) якщо 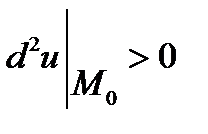 , то точка М0 точка локального мінімуму,
, то точка М0 точка локального мінімуму,
б) якщо 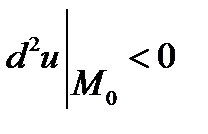 , то точка М0 точка локального максимуму,
, то точка М0 точка локального максимуму,
2) якщо другий диференціал 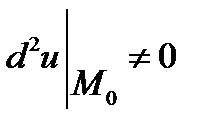 і є знакозмінною квадратичною формою незалежних змінних dx1, dx2, ….dxn, то точка М0 не є точкою локального екстремуму.
і є знакозмінною квадратичною формою незалежних змінних dx1, dx2, ….dxn, то точка М0 не є точкою локального екстремуму.
3) якщо 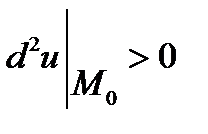 , екстремум може бути, а може й не бути (потрібне додаткове дослідження).
, екстремум може бути, а може й не бути (потрібне додаткове дослідження).
Запишемо вираз для 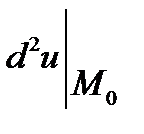 у вигляді
у вигляді
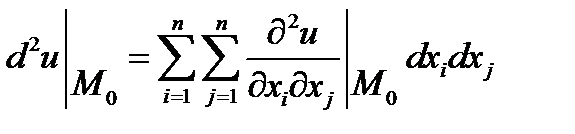
Введемо позначення для частинних похідних другого порядку, які обчислюються в точці М0
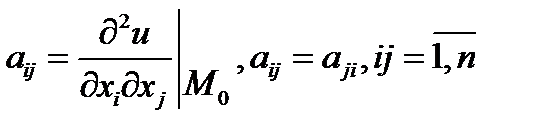
Тоді
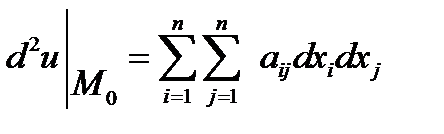
є квадратичною формою змінних dx1, dx2, ….dxn, з матрицею
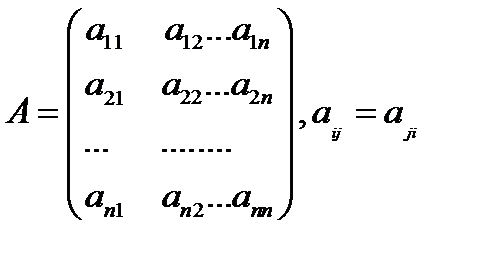
Головні кутові мінори цієї матриці
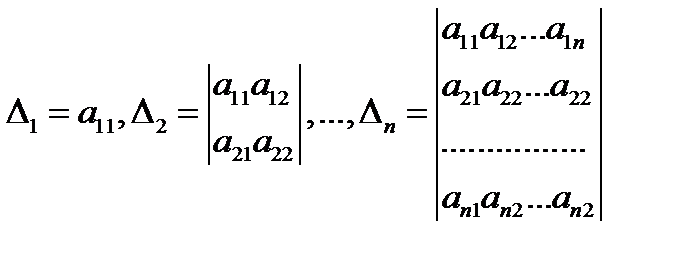
Згідно з критерієм Сильвестра знаковизначеності квадратичної форми, квадратична форма додатно визначена, якщо 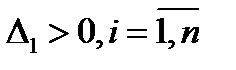 , від`ємно визначена, коли всі головні кутові мінори непарного порядку від`ємні, парного – додатні.
, від`ємно визначена, коли всі головні кутові мінори непарного порядку від`ємні, парного – додатні.
На підставі критерію Сильвестра можна визначити знак другого диференціала в точці М0, тобто 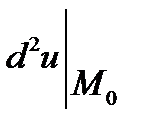 , враховуючи знаки головних кутових мінорів матриці відповідної квадратичної форми. Отже, маємо,
, враховуючи знаки головних кутових мінорів матриці відповідної квадратичної форми. Отже, маємо,
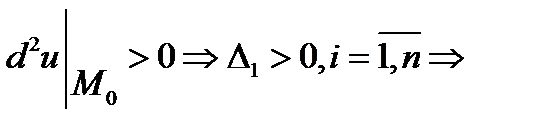 точка локального мінімуму
точка локального мінімуму
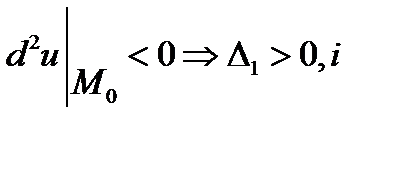 парне
парне 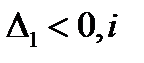 не парне,
не парне, 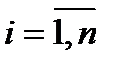
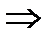 точка локального максимуму;
точка локального максимуму;
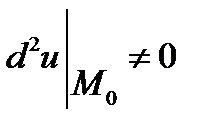 критерій Сильвестра не справджується –точка
критерій Сильвестра не справджується –точка  -не є точкою локального екстремуму;
-не є точкою локального екстремуму;
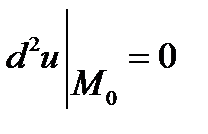 потрібне додаткове дослідження.
потрібне додаткове дослідження.
Для функцій двох змінних z = f(x,y) другий диференціалмає вигляд
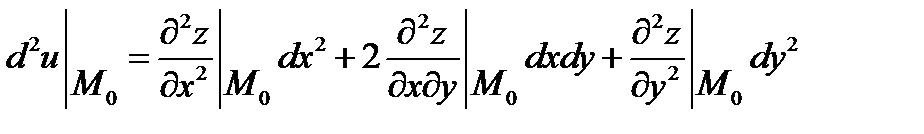
Позначивши
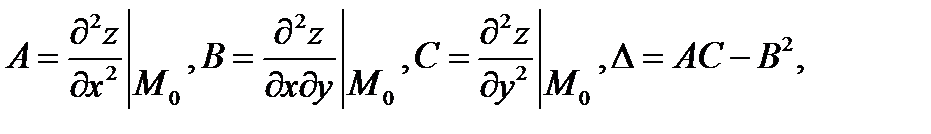
1)якщо  >0, то функція z = f(x, y) має в точці М0 екстремум, зокрема, мінімум при А>0, максимум - при А<0,
>0, то функція z = f(x, y) має в точці М0 екстремум, зокрема, мінімум при А>0, максимум - при А<0,
2) якщо  <0, екстремум у точці М0 відсутній,
<0, екстремум у точці М0 відсутній,
3) якщо  =0, потрібне додаткове дослідження.
=0, потрібне додаткове дослідження.
Знайти екстремум функції
Z=ex-y(x2-2y2)
ОДЗ: ¾ R
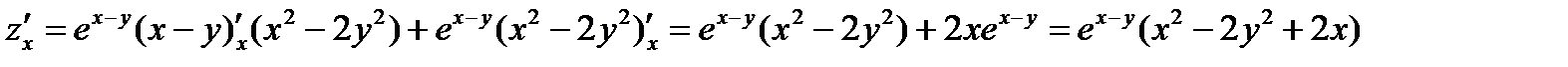
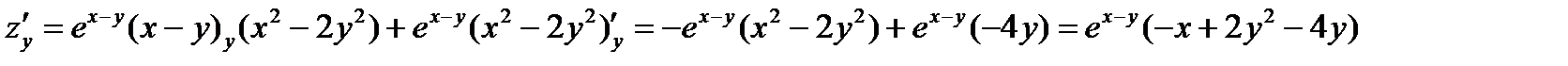
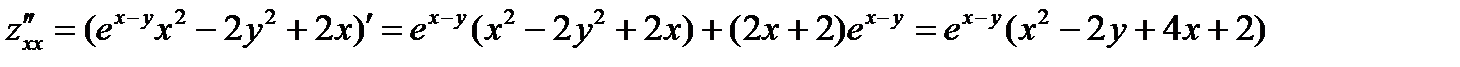

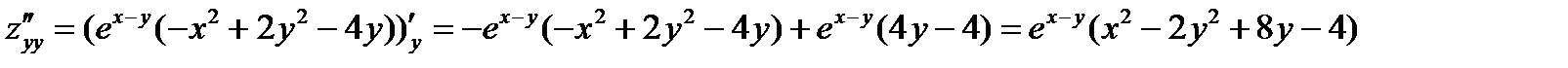
Знаходимо стаціонарні точки використовуючи умови екстремуму
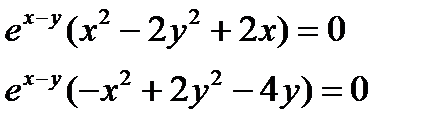
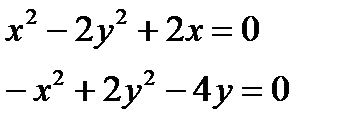 (методом додавання)
(методом додавання)
2x-4y=0
x=2y
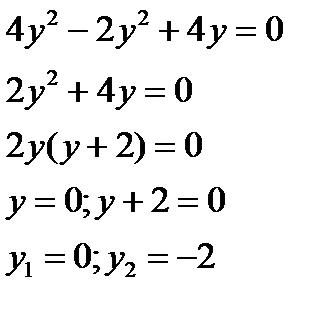
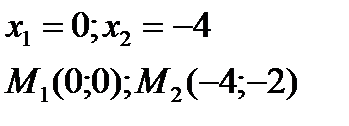
Стаціонарні точки
4)Для кожної точки окремо перевіряємо достатні умови екстремуму
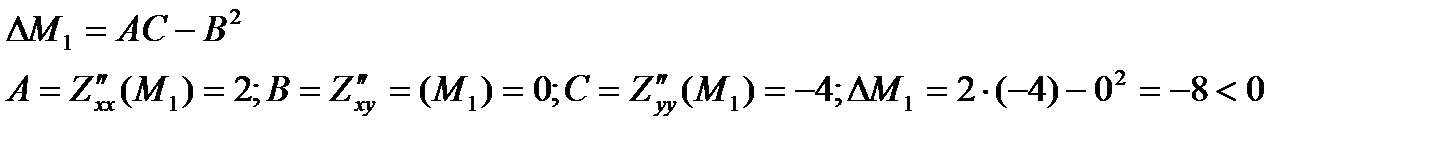
М1 ¾не є точкою екстремуму
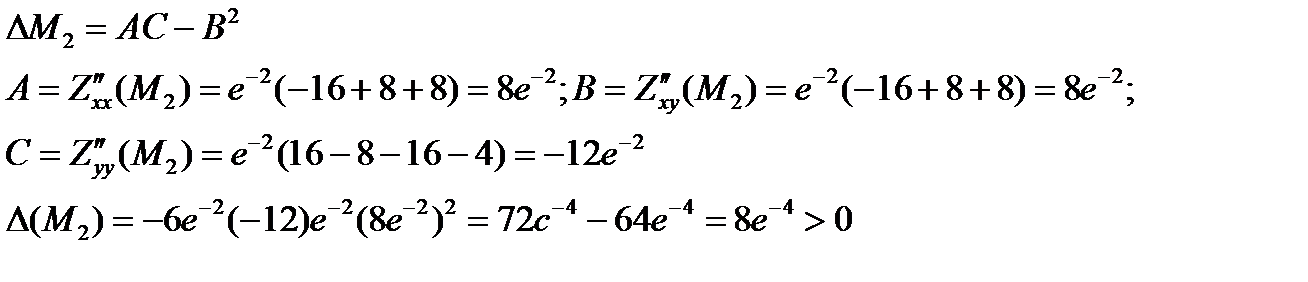
А>0; M2 ¾ точка max
| 4 |
Побудова лінійної залежності між двома змінними величинами значення яких додається в таблиці
| X | X1 | x2 
| … | xi | xn |
| Y | Y1 | y2 | yi | yn |
у = kx+b
k1,b ¾?
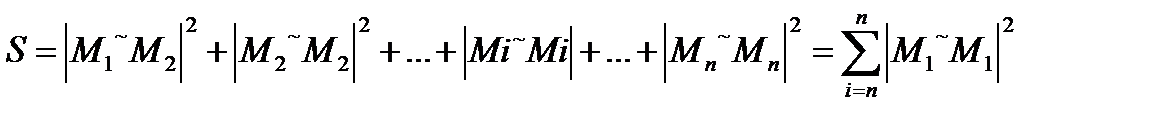

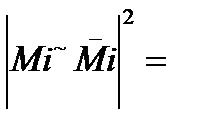

 Знайдемо частинні похідні
Знайдемо частинні похідні

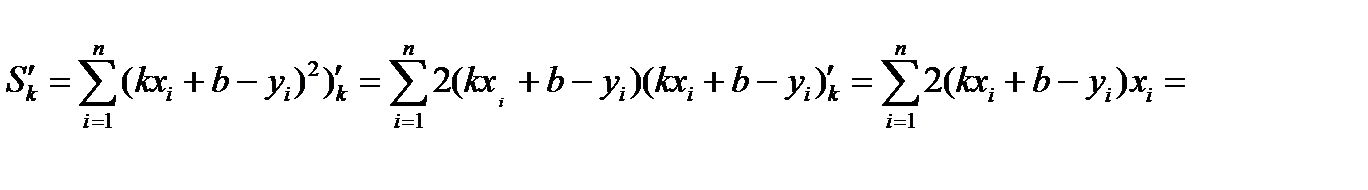
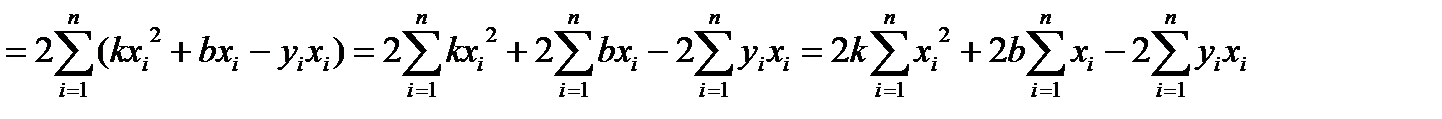
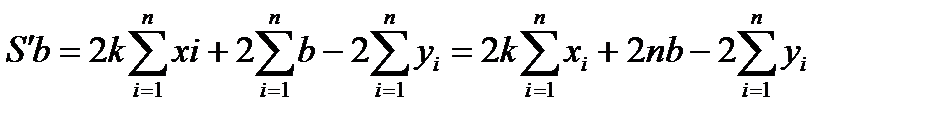
Перевіряємо достатні умови екстремуму для точки М.
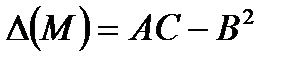
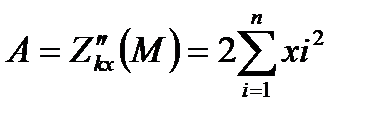
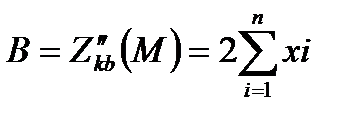
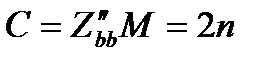
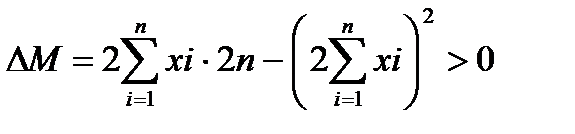
A>0, тому точка М-точка мінімуму (min).таким чином функція S=S(k,b) при k,b знайдених за формулами 6.7 приймає мінімальне значення.
Для побудови лінійної залежності y = kx+b потрібно:
1) за даними таблиці скласти систему рівнянь 6.6;
2) розв’язати її за формулами Крамера і записати лінійну залежність
Приклад 1.
| x | 1 | 3 | 4 | 2 | |
| y | 4 | 8 | 2 | 5 |
у = kx+b
Складемо розрахункову таблицю:
| xi | yi | xi2 | xi× yi | |
| 1 | 4 | 1 | 4 | |
| 3 | 8 | 9 | 24 | |
| 5 | 3 | 25 | 15 | |
| 4 | 2 | 16 | 8 | |
| 2 | 5 | 4 | 10 | |
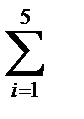
| 15 | 22 | 55 | 61 |
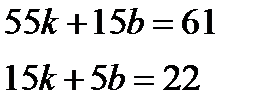

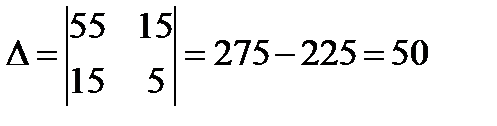 ;
; 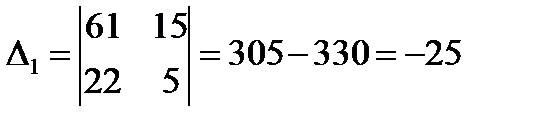 ;
; 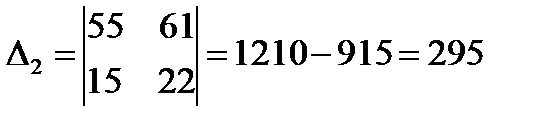
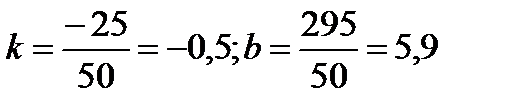
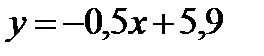
4.2 Побудова квадратичної залежності між двома змінними величинами
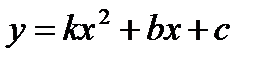
Для знаходження k,b,c. Отримаємо систему рівнянь. 
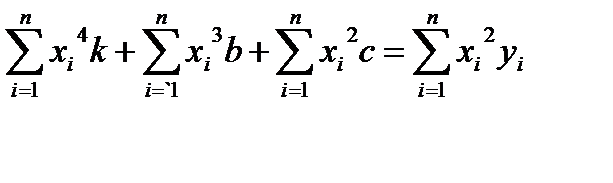
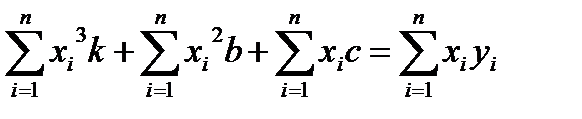 (6.8)
(6.8)
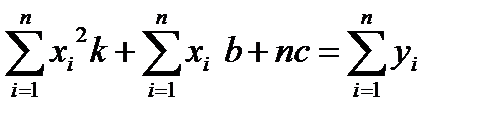
Приклад 2.
За прикладом 1 скласти квадратичну залежність
| xi | yi | xi2 | xi× yi | xi3 | xi4 | xi2×yi | |
| 1 | 4 | 1 | 4 | 1 | 1 | 4 | |
| 3 | 8 | 9 | 24 | 27 | 81 | 72 | |
| 5 | 3 | 25 | 15 | 125 | 625 | 75 | |
| 4 | 2 | 16 | 8 | 64 | 256 | 32 | |
| 2 | 5 | 4 | 10 | 8 | 16 | 20 | |
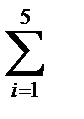
| 15 | 22 | 55 | 61 | 225 | 979 | 203 |
979k+225b+55c=203
55b+15c=61
55k+15b+5c=22
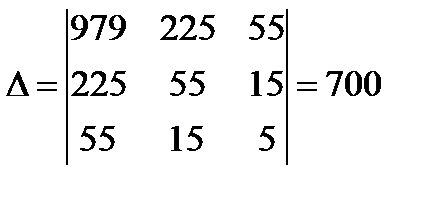 ;
; 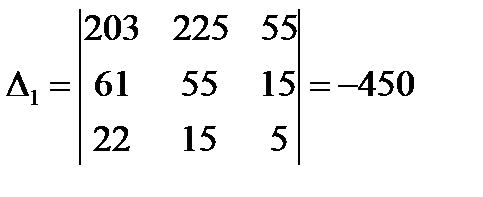 ;
; 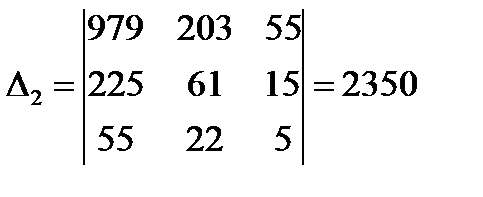 ;
;
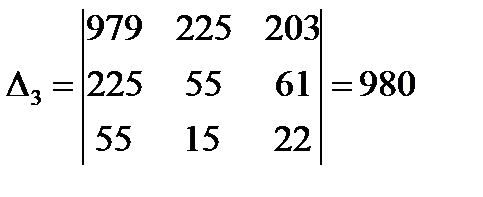 ;
;
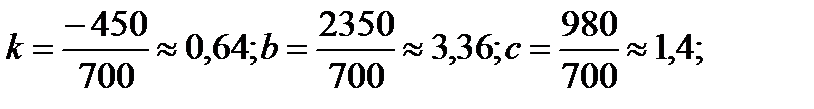
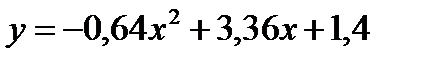
| 5 |
Умовний екстремум функцій багатьох змінних. Умовним екстремумом функції u = f(x1, х2, ….хn) називається екстремумом цієї функції, який досягається за умови, що змінні x1, х2, ….хn зв»язані з рівняннями зв»язку
Тобто задача ставиться так: знайти екстремум функції
u = f(x1, х2, ….хn) (6.9)
за умови, що
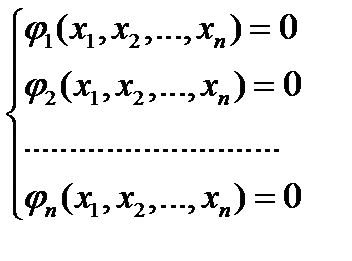 (6.10)
(6.10)
Для розв»язання такої задачі використовується метод множників Лагранжа, згідно з яким задача знаходження умовного екстремуму зводиться до дослідження на звичайний екстремум функції Лагранжа
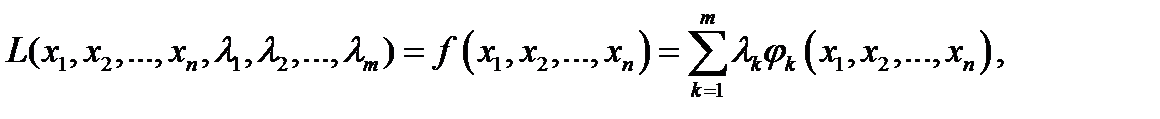 (6.11)
(6.11)
Де 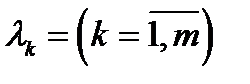 називаються множниками Лагранжа.
називаються множниками Лагранжа.
Необхідні умови умовного екстремуму виражаються системою n + m рівнянь
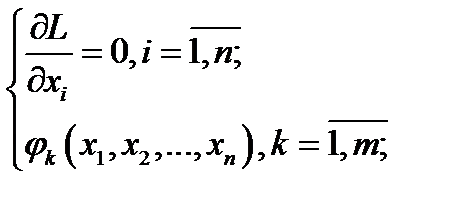 (6.12)
(6.12)
Розв»язки цієї системи - стаціонарні точки функції Лагранжа.
Достатні умови умовного екстремуму можна встановити за знаком диференціала другого порядку функції Лагранжа з урахуванням рівнянь зв»язку.
Зокрема, для випадку відшукання екстремуму функції двох змінних
z = f(x, y) (6.13)
за умови, що
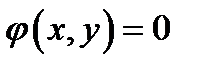 (6.14)
(6.14)
функція Лагранжа має вигляд
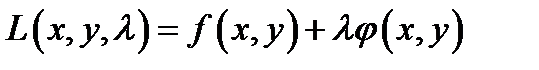 (6.15)
(6.15)
а відповідна система рівнянь для знаходження стаціонарної точки така
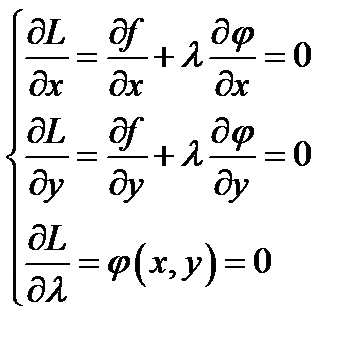
З цієї системи знаходяться невідомі 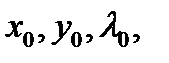 де
де 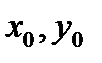 - координати точки, в якій можливий умовний екстремум.
- координати точки, в якій можливий умовний екстремум.
Достатні умови умовного екстремуму такі:
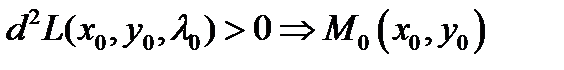 -точка умовного мінімуму;
-точка умовного мінімуму;
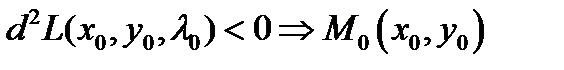 -точка умовного максимуму
-точка умовного максимуму
при дослідженні знаку 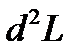 слід мати на увазі, що диференціали змінних dx, dy в
слід мати на увазі, що диференціали змінних dx, dy в 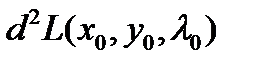 залежні і ця залежність диктується рівняннями зв»язку.
залежні і ця залежність диктується рівняннями зв»язку.
Крім того, оскільки 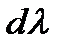 не є звичайною змінною, то при визначенні знака
не є звичайною змінною, то при визначенні знака 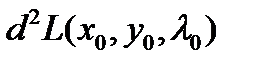 величина
величина 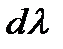 не враховується, тобто вважається
не враховується, тобто вважається
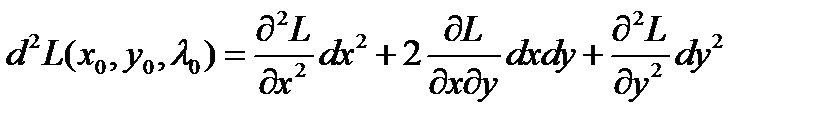
| 6 |
Тому, для того щоб знайти найбільше та найменше значення функції в замкненій області, треба:
1) знайти стаціонарні точки, що розташовані в заданій області, і обчислити значення функції в цих точках;
2) знайти найбільше та найменше значення функції на лініях, що утворюють межу області;
3) з усіх знайдених значень вибрати найбільше та найменше.
Дослідити на екстремум функцію
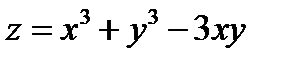
Знаходимо частинні похідні функції z першого порядку.
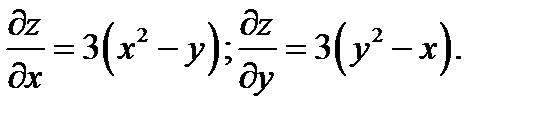
Прирівнюючи нулю ці похідні,отримуємо систему для визначення стаціонарних точок:
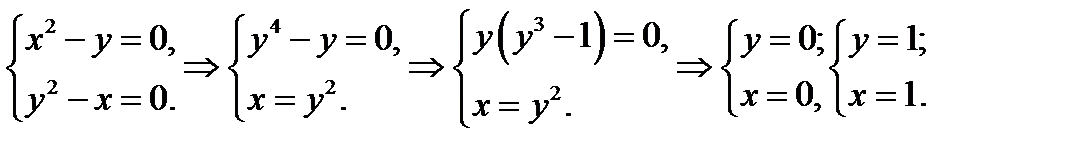
Маємо дві стаціонарні точки 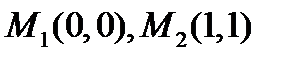
Для перевірки достатніх умов екстремуму знаходимо частинні похідні другого порядку
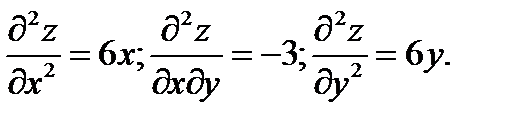
Тоді для точки 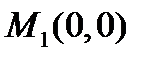 маємо:
маємо:
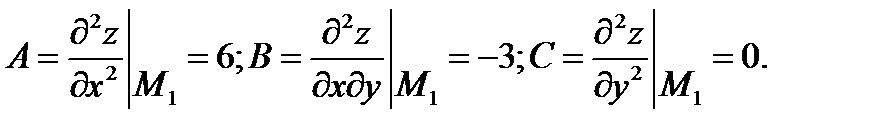
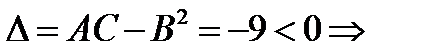 точка
точка 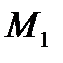 не є точкою екстремуму.
не є точкою екстремуму.
Для точки 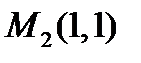 маємо:
маємо:
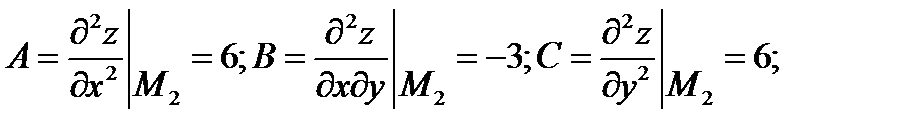
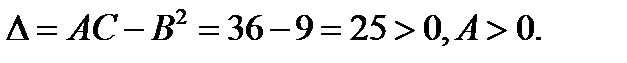 отже точка
отже точка 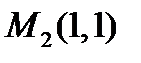 -точка локального мінімуму.
-точка локального мінімуму.
Знайдемо значення функції z у цій точці
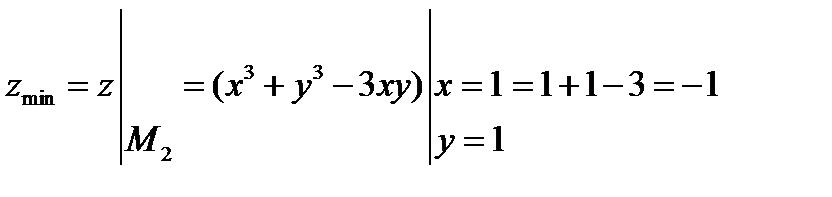
Зауважимо,що для встановлення типу стаціонарної точки можна також безпосередньо досліджувати знак другого диференціалу як квадратичної форми змінних
dx i dy, використовуючи метод виділення повного квадрату.
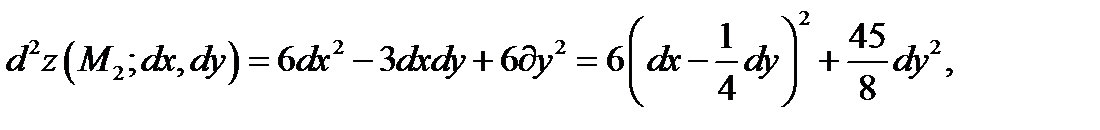
Звідки видно,що для будь яких dx i dy не рівних одночасно нулю, 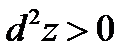 ,отже,точка
,отже,точка 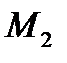 - точка мінімуму.
- точка мінімуму.
Приклад. Знайти найбільше та найменше значення функції 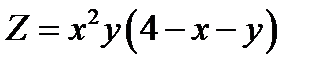 в трикутнику, обмеженому лініями x=0, y=0, x+y=6
в трикутнику, обмеженому лініями x=0, y=0, x+y=6
Розв`язання. Спочатку знайдемо критичні точки всередині області:
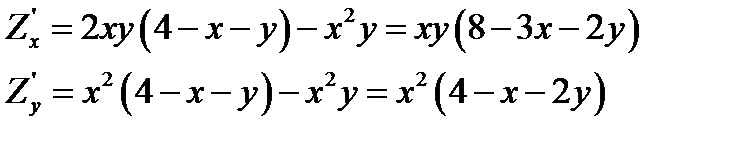
Згідно з необхідними умовами існування екстремуму функції маємо систему рівнянь
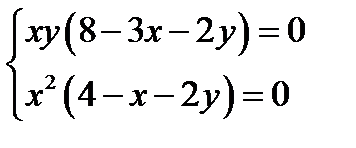
Всередині області 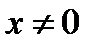 та
та 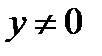 тому
тому
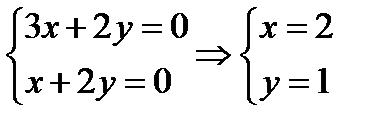
В критичній точці 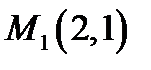 маємо
маємо 
Тепер проводимо дослідження функції на межі трикутника.
На прямій x+y=6 змінна y=6-x і функція Z приймає вигляд
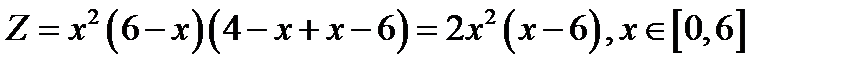
Знайдемо найбільше та найменше значення цієї функції однієї змінної x на замкненому відрізку [0,6]: 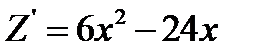
Із рівності  знаходимо: 6x(x-4)=0,звідси випливає,що
знаходимо: 6x(x-4)=0,звідси випливає,що 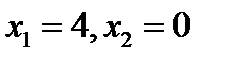 .
.
Z(4)=-64;при x=0 та x=6 Z(0)=0;Z(6)=0.
На прямій y=0 маємо Z=0.
Отже,задана функція Z має найбільше значення в точці 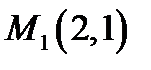 всередині області,найменше значення – в точці
всередині області,найменше значення – в точці 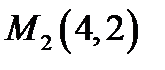 на межі області.
на межі області.
Найбільше значення 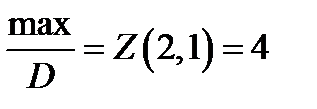
Найменше значення 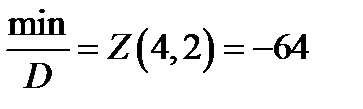
 2020-07-12
2020-07-12 131
131







