Дизъюнктивные и конъюнктивные нормальные формы
Если x – логическая переменная, 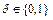 , то выражение
, то выражение  называется литерой.
называется литерой.
Элементарной конъюнкцией (конъюнктом) называется конъюнкция литер.
|
 =x
=x  p/z
p/z  y
y  x
x  p
p  z
z  x
x  y
y  z,
z,
 =p
=p  y
y  y/x
y/x  z
z  p
p  y
y  z,
z,
 =p/z
=p/z  x
x  y
y  y
y  p
p  (x
(x  y
y  z),
z),
 =y
=y  z
z  p
p  x
x  z
z  p
p  y/y
y/y  z,
z,
 =z
=z  y
y  p
p  x
x  z
z  p
p  z
z  y/x,
y/x,
 =x/y
=x/y  p
p  x
x  z
z  x
x  y
y  z
z  x
x 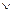 z,
z,
 =z
=z  y
y  x
x  z
z  p
p  x
x  z/y
z/y  p,
p,
 =y
=y  z
z  p
p  x
x  z
z  p
p  y/p
y/p  z,
z,
 =p
=p  x/z
x/z  y
y  p
p  z
z  y
y 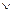 z
z  x,
x,
 =x/y
=x/y  z
z  p
p  x
x  y
y  z
z  p
p  y
y  z,
z,
 =z
=z  p
p  y
y  z
z 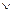 x
x  p
p  y
y  z/x,
z/x,
 =x/z
=x/z 
 y
y  x
x 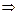 z
z  p
p  y
y  p,
p,
 =x
=x  y
y  x
x  p
p  x/y
x/y  z
z 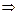 p
p  z,
z,
 =p/z
=p/z  y
y  x
x 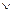 p
p  z
z  y
y  z
z  x,
x,
 =y
=y  z
z  p
p  x
x  x
x  y/z
y/z  x
x  y
y  p,
p,
 =z/x
=z/x  y
y 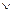 p
p  x
x  y
y  z
z  x
x  p,
p,
 =x
=x  y
y  z
z  p/x
p/x  y
y  x
x  z
z  (y
(y  p),
p),
 =x/z
=x/z  p
p  x
x  p
p  x
x  z
z  p
p  y,
y,
 =x/z
=x/z 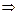 y
y  p
p  x
x  y
y  z
z  p/x
p/x  z,
z,
 =y/p
=y/p  x
x  y
y  p
p  z
z  x
x  z
z  x,
x,
 =p
=p  y
y  z
z  p
p  y
y  z/x
z/x  p,
p,
 =p
=p  z
z  y
y  z
z  p/x
p/x  z
z  y
y  x,
x,
 =x
=x  y
y  z
z  x
x  y
y 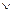 z
z  y
y  p/x,
p/x,
 =z/x
=z/x  p
p  y
y  x
x  y
y  z
z  x
x  p,
p,
 =y
=y  x
x  z
z  p
p  y
y  x
x  y
y  z/x
z/x  p,
p,
 =z
=z  y
y  x/y
x/y  z
z  x
x  y
y  z
z  p,
p,
 =x
=x  y
y  z
z  x
x  p
p  y/z
y/z  x
x  y,
y,
 =x
=x  y
y  z
z  p
p  x
x  y/x
y/x  z
z  y,
y,
|
 =p
=p  x
x  y/z
y/z  p
p  y
y  x
x  z
z 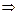 y
y  p.
p.
Пример 1-2. Пусть требуется представить в виде таблицы следующую функцию:  &
& 
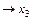 .
.
Будем вычислять функцию  последовательно.
последовательно.

| 
| 
| 
| 
| 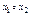
| [ ] | 
| { } | 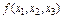
|
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
 2020-07-12
2020-07-12 105
105








