Теория ортогональных сигналов

Введя во множестве сигналов структуру линейного пространства, определив норму и метрику, мы, тем не менее, лишены возможности вычислить такую характеристику, как угол между двумя векторами. Это удается сделать, сформулировав важнейшее понятие скалярного произведения элементов линейного пространства.

Скалярное произведение сигналов. Напомним, что если в обычном трехмерном пространстве известны два вектора А и B, то квадрат модуля их суммы

,          (2.10)

где 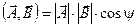- скалярное произведение этих векторов, зависящее от угла y между ними.

Действуя по аналогии, вычислим энергию суммы двух сигналов u и v:

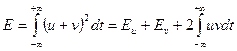(2.11)

В отличие от самих сигналов их энергии неаддитивны - энергия суммарного сигнала содержит в себе так называемую взаимную энергию:

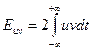
Сравнивая между собой формулы (2.10) и (2.11), определим скалярное произ­ведение
вещественных сигналов   u и v:

                   (2.12)

а также косинус угла между ними:

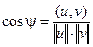.                   (2.13)

 

Скалярное произведение обладает свойствами:

1. (u, u) ³ 0;                                          (2.14)

2. (u, v) = (v, u);

3. (l u, v) = l(u, v), где l - вещественное число;

4. (u + v, w) = (u, w) + (v, w).

Линейное пространство с таким скалярным произведением, полное в том смысле, что оно содержит в себе все предельные точки любых сходящихся последовательностей векторов из этого пространства, называется вещественным гильбертовым пространством H.

Давид Гильберт (1862-1943) - известный немецкий математик.

Справедливо фундаментальное неравенство Коши-Буняковского

.                (2.15)

Если сигналы принимают комплексные значения, то можно определить комплексное гильбертово пространство, введя в нем скалярное произведение по формуле:

,               (2.16)

такое, что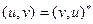

Пример 6. Имеются два смещенных во времени экспоненциальных импульса напряжения:

,

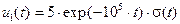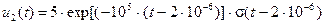
Найти скалярное произведение данных сигналов, а также угол y между ними.

Энергии этих двух сигналов одинаковы:

.

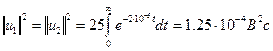Скалярное произведение

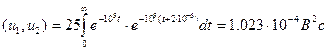Отсюда cos(y)=0.819 и y=35°

 

Ортогональные сигналы и обобщенные ряды Фурье. Два сигнала u и v называются ортогональными, если их скалярное произведение, а значит, и взаимная энергия равны нулю:

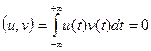             (2.17)

Пусть H - гильбертово пространство сигналов с конечным значением энергии. Эти сигналы определены на отрезке времени
 [ t₁, t₂ ], конечном или бесконечном.
Предположим, что на этом же отрезке задана бесконечная система ортогональных друг другу функций { u₀, u₁, u₂,..., u_n,...}, которые обладают единичными нормами:

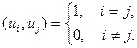                (2.18)

Говорят, что при этом в пространстве сигналов задан ортонормированный базис.

Разложим произвольный сигнал s (t)Î H в ряд:

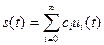           (2.19)

Представление (2.19) называется обобщенным рядом Фурье сигнала s (t) в выбранном базисе.

Коэффициенты данного ряда находят следующим образом. Возьмем базисную функцию u _k с произвольным номером k, умножим на нее обе части равенства (2.19) и затем проинтегрируем результаты по времени:

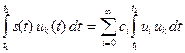(2.20)

Ввиду ортонормированности базиса в правой части (1.28) останется только член суммы
с номером i = k, поэтому

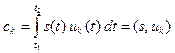     (2.21)

На геометрическом языке интерпретация формулы (2.21) такова: коэффициент обобщенного ряда Фурье есть проекция вектора на базисное направление.

Возможность представления сигналов посредством обобщенных рядов Фурье является фактом большого принципиального значения. Вместо того чтобы изучать функциональную зависимость в несчетном множестве точек, мы получаем возможность характеризовать эти сигналы в счетной (но, вообще говоря, бесконечной) системой коэффициентов обобщенного ряда Фурье c _k.

Напомним, что гильбертово пространство сигналов, по определению, обладает важным свойством полноты:

- если предельное значение суммы

 

существует, то этот предел сам является некоторым элементом гильбертова пространства.

В полном функциональном пространстве норма ошибки аппроксимации монотонно убывает с ростом N - числом учитываемых членов ряда. Выбирая N достаточно большим, всегда можно снизить норму ошибки до любой приемлемо малой величины.