Геометрические методы в теории сигналов

При решении многих теоретических и прикладных задач радиотехники возникают такие вопросы:

1) в каком смысле можно говорить о величине сигнала, утверждая, например, что один сигнал значительно превосходит другой;

2) можно ли объективно оценивать, насколько два неодинаковых сигнала "похожи" друг на друга?

В XX в. был создан функциональный анализ - раздел математики, обобщающий наши интуитивные представления о геометрической структуре пространства.

Оказалось, что идеи функционального
анализа дают возможность создать стройную теорию сигналов, в основе которой лежит концепция сигнала как вектора в специальном образом сконструированном бесконечномерном пространстве.

Линейное пространство сигналов. Пусть M ={ s ₁(t), s ₂(t),...} - множество сигналов. Причина объединения этих объектов - наличие некоторых свойств, общих для всех элементов множества M.

Пример 1. Множество M образовано
всевозможными аналоговыми сигналами, отличными от нуля лишь на интервале времени (0, 15 мкс) и равными нулю вне этого интервала.

Пример 2. Множество M состоит из сигналов вида s_n (t) = A_n cos(w _nt + j_n) -гар­монических колебаний, отличающихся своими амплитудами, частотами и начальными фазами.

Исследование свойств сигналов, образующих такие множества, становится особенно плодотворным тогда, когда удается выражать одни элементы множества через другие элементы. Принято говорить, что множество сигналов наделено при этом определенной структурой. Выбор той или иной структуры должен быть продиктован физическими соображениями. Так, применительно к электрическим колебаниям известно, что они могут складываться, а также умножаться на произвольный масштабный коэффициент. Это дает возможность
ввести в множествах сигналов структуру линейного пространства.

Множество сигналов M образует вещественное линейное пространство, если справедливы следующие аксиомы:

1. Любой сигнал uÎ M при любых t принимает лишь вещественные значения.

2. Для любых сигналов uÎ M и vÎ M существует их сумма s = u+v, причем s также содержится в M. Операция суммирования коммутативна: u+v = v+u и ассоциативна: u+ (v+x) = (u+v) +x.

3. Для любого сигнала sÎ M и любого вещественного числа a определен сигнал f = a s Î M.

4. Множество M содержит особый нулевой элемент Æ, такой, что s+ Æ =s для всех sÎ M.

Если математические модели сигналов принимают комплексные значения, то, допуская в аксиоме 3 умножение на комплексное число, приходим к понятию комплексного линейного пространства.

Введение структуры линейного пространства является первым шагом на пути к геометрической трактовке сигналов. Элементы линейных пространств часто называют векторами, подчеркивая аналогию свойств этих объектов и обычных трехмерных векторов.

Ограничения, накладываемые аксиомами линейного пространства, достаточно жестки. Далеко не каждое множество сигналов оказывается линейным пространством.

Пример 3. Множество M состоит из всевозможных прямоугольных видеоимпуль­сов напряжения, существующих на интервале времени (0, 20 мкс), причем амплитуды импульсов не превышают 10В.

Сложив, например, импульсы с амплитудами 6В и 8В, получаем импульс, не принадлежащий множеству M. Поэтому множество M не является линейным пространством

Понятие координатного базиса. Как и в обычном трехмерном пространстве, в линейном пространстве сигналов можно выделить специальное подмножество, играющее роль координатных осей.

Говорят, что совокупность векторов
 { e ₁, e ₂, e ₃,...}, принадлежащих M, является
линейно независимой, если равенство

å a_i e_i =Æ

возможно лишь в случае одновремен­ного
обращения в нуль всех числовых коэффициентов a_i.

Система линейно независимых векторов образует координатный базис в линейном пространстве.

Если дано разложение некоторого сигнала s (t) в виде

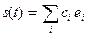
то числа { c ₁, c ₂, c ₃,...} являются проекциями сигнала s (t) относительно выбранного базиса. Какой либо элемент координатного базиса не может быть выражен в виде линейной комбинации оставшихся элементов базиса.

В задачах теории сигналов число базисных векторов, как правило, неограни­ченно велико. Такие линейные пространства называют бесконечномерными. Естест­венно, что теория этих пространств не может быть вложена в формальную схему линейной алгебры, где число базисных векторов всегда конечно.

Пример 4. Линейное пространство образовано сигналами, которые описываются многочленами неограниченно высокого порядка:

  

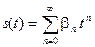
(такие функции называются аналитическими). Координатным базисом в этом пространстве служит система одночленов
{ e ₁=1; e ₂= t; e ₃= t ²;...}.

Нормированное линейное пространство. Энергия сигнала. Для того чтобы продолжить и углубить геометрическую трактовку теории сигналов, необходимо ввести новое понятие, которое по своему смыслу соответствует длине вектора. Это позволит не только придать точный смысл высказыванию типа "первый сигнал больше второго", но и указать, на сколько он больше.

Длину вектора в математике называют его нормой. Линейное пространство сигналов L называют нормированным, если каждому вектору s (t) Î L однозначно сопоставлено число ÷ç s ÷ç - норма этого вектора, причем выполняются следующие аксиомы нормированного пространства:

1. Норма неотрицательна, т.е. ÷ç s ÷ç³0. Норма ÷ç s ÷ç= 0 тогда и только тогда, если s =0.

2. Для любого числа a справедливо равенство

÷ç as ÷ç=ç a ÷÷ç s ÷ç.

3. Если s (t) и p (t) - два вектора из L, то
выполняется неравенство треугольника:

÷ç s+p ÷ç £ ÷ç s ÷ç+÷ç p ÷ç.

Данная аксиоматика в равной степени относится как к аналоговым, так и к дискретным сигналам.

Можно предложить разные способы введения нормы сигналов. В радиотехнике чаще
всего полагают, что вещественные аналоговые сигналы имеют норму

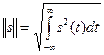              (2.8)

(из двух возможных значений корня выбирается положительное). Для комплексных сигналов норма

           

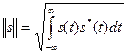
где * - символ комплексного сопря­жения.

Квадрат нормы называется энергией сигнала:

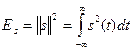                 (2.9)

Именно такая энергия выделяется в резисторе с сопротивлением 1 Ом, если на его зажимах существует напряжение s (t).

Если сигнал дискретен, то операция интегрирования должна быть заменена суммированием по всем отсчетам сигнала.

Определять норму сигнала с помощью
формулы (2.8) целесообразно по следующим причинам:

· В радиотехнике о величине сигнала часто судят, исходя из суммарного энергетического эффекта, например, коли­чес­т­ва теплоты, выделяемой в резисторе.

· Энергетическая норма оказывается "нечувствительной" к изменениям формы сигнала, может быть, и значительным, но происходящим на коротких отрезках времени.

Линейное нормированное пространство с конечной величиной нормы вида (2.8) носит название пространства функций с интегрируемым квадратом и кратко обозначается L ₂.

  Метрическое пространство. Теперь необходимо ввести еще одно фундаментальное понятие, которое обобщало бы наше обычное представление о расстоянии между точками в пространстве.

Говорят, что линейное пространство L становится метрическим пространством, если каждой паре элементов u, v Î L  сопоставлено неотрицательное число r (u, v), называемое метрикой, или расстоянием между этими элементами. Метрика, независимо от способа ее определения, должна подчиняться аксиомам метрического пространства:

1. r (u, v)= r (v, u) (рефлексивность метрики).

2. r (u, u)=0  для любых uÎ L.

3. Каков бы ни был элемент wÎ L, всегда

r(u, v)£ r(u, w)+ r(w, v).

Обычно метрику определяют как норму
разности двух сигналов:

r(u, v) = ÷ç u - v ÷ç.         

Норму, в свою очередь, можно понимать как расстояние между выбранным элементом
пространства и нулевым элементом:   

÷ç u ÷ç = r(u,Æ).           

Зная метрику, можно судить о том, насколько хорошо один из сигналов аппроксимирует другой.

Пример 5. Сигнал u (t) представляет собой отрезок синусоиды, обращающийся в нуль на концах отрезка [0, T ]. Высота импульса U известна. Выбрать амплитуду A прямоугольного импульса v (t) той же длительности так, чтобы расстояние между этими двумя сигналами было минимальным.

Сигнал u (t) представляется формулой:

u (t)= U sin(p t / T), 0 £ t £ T.

Квадрат расстояния между сигналами:

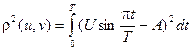
Проведя интегрирование, имеем

r ²(u, v) = U ² T /2 - 4 AUT /p+ A ² T

Исследуя это выражение на экстремум,
убеждаемся, что минимум расстояния будет достигнут, если A = 2 U /p» 0.637 U. При этом

r ²_min(u, v) = U ² T (1/2-4p²)» 0.095 U ² T,

r _min(u, v)» 0.308 U Ö T.

То, что в точке экстремума действительно достигается минимум, вытекает из положительности второй производной исследуемой функции.

Заметим, что энергия синусоидального импульса:

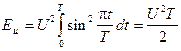
а его норма ÷ç u ÷ç» 0.707 U Ö T.

Итак, при выбранной метрике минимально достижимое расстояние между рас­сма­три­ваемыми сигналами составляет 44% от нормы синусоидального импульса.