Знакоположительным рядом называется ряд вида
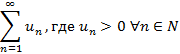
Теорема 1 – Признак сравнения: Пусть для знакоположительных рядов 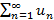 и
и 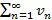 выполняется
выполняется 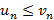 , тогда справедливо следующее: из сходимости большего следует сходимость меньшего или из расходимости меньшего следует расходимость большего.
, тогда справедливо следующее: из сходимости большего следует сходимость меньшего или из расходимости меньшего следует расходимость большего.
Теорема 2 - Предельный признак: Если для знакоположительных рядов 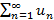 и
и 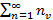 существует конечный предел вида
существует конечный предел вида 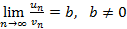 , тогда ряды ведут себя одинаково: оба сходятся или оба расходятся.
, тогда ряды ведут себя одинаково: оба сходятся или оба расходятся.
Теорема 3 – Признак Даламбера: Пусть для знакоположительного ряда 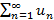 выполняется
выполняется 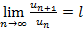 , тогда если
, тогда если 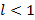 – ряд сходится,
– ряд сходится, 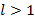 – ряд расходится,
– ряд расходится, 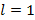 – признак не работает.
– признак не работает.
Теорема 4 – Признак Коши: Пусть для знакоположительного ряда 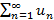 существует предел вида
существует предел вида 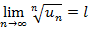 , тогда если
, тогда если 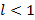 – ряд сходится,
– ряд сходится, 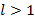 – ряд расходится,
– ряд расходится, 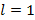 – признак не работает.
– признак не работает.
Теорема 5 – Интегральный признак Коши: Пусть для знакоположительного ряда 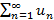 найдена функция
найдена функция  , определенная на отрезке
, определенная на отрезке 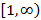 со свойствами:
со свойствами: 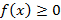 ,
,  монотонно убывает,
монотонно убывает, 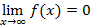 ,
, 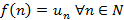 . Тогда ряд и несобственный интеграл
. Тогда ряд и несобственный интеграл 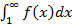 ведут себя одинаково: оба сходятся или оба расходятся.
ведут себя одинаково: оба сходятся или оба расходятся.
Знакопеременные и знакочередующиеся ряды
Ряд 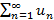 , у которого присутствуют и положительные и отрицательные слагаемые называется знакопеременным.
, у которого присутствуют и положительные и отрицательные слагаемые называется знакопеременным.
Ряды вида 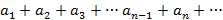 , где
, где 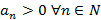 называется знакочередующимся.
называется знакочередующимся.
Теорема – Признак Лейбница: Если для модулей членов знакочередующегося ряда выполняются следующие условия: 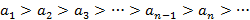 и
и 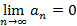 , тогда ряд сходится и его сумма по модулю оценивается как
, тогда ряд сходится и его сумма по модулю оценивается как 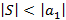 .
.
Если у знакопеременного ряда сходится ряд из модулей, тогда сам исходный ряд также сходится (обратное высказывание неверно). Если у сходящегося знакопеременного ряда ряд из модулей сходится, тогда исходный ряд называется абсолютно сходящимся. Если ряд из модулей расходится – условно сходящимся.
Если ряд сходится абсолютно, тогда перестановка бесконечного числа слагаемых не влияет на сумму. Перестановка слагаемых у условно сходящегося ряда может привести к любому значению суммы или привести к расходимости ряда.
Функциональные ряды
Бесконечная сумма вида 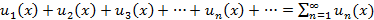 называется функциональным рядом. Если у функционального ряда зафиксировать точку
называется функциональным рядом. Если у функционального ряда зафиксировать точку 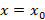 , тогда ряд станет числовым.
, тогда ряд станет числовым.
Множество всех значений x, при которых функциональный ряд сходится называется областью сходимости ряда. Аналогично числовым рядам можно ввести частичные суммы следующего вида
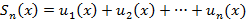
Если x принадлежит области сходимости, тогда сумма ряда 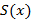 определена на области сходимости ряда
определена на области сходимости ряда
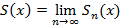
Степенные ряды
Функциональный ряд называется степенным, если элементы ряда определены степенной функцией
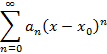
Частный случай при 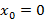 , тогда степенной ряд примет вид
, тогда степенной ряд примет вид
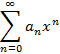
У степенного ряда вида 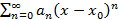 всегда существует число R со следующим свойством: ряд сходится на интервале
всегда существует число R со следующим свойством: ряд сходится на интервале 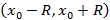 и расходится на лучах
и расходится на лучах 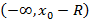 и
и 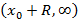 . Число R называется радиусом сходимости, а интервал
. Число R называется радиусом сходимости, а интервал 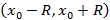 – радиусом сходимости. Радиус сходимости можно найти из следующих соотношений
– радиусом сходимости. Радиус сходимости можно найти из следующих соотношений
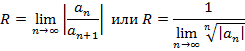
На концах интервала сходимости ряд может быть сходящимся, так и расходящимся.
Если степенной ряд сходится на своем интервале сходимости к функции суммы ряда 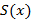 , тогда справедливы следующие высказывания:
, тогда справедливы следующие высказывания:
1. 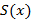 непрерывна на интервале сходимости;
непрерывна на интервале сходимости;
2. Ряд можно почленно дифференцировать
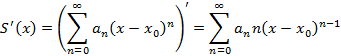
3. Ряд можно почленно интегрировать
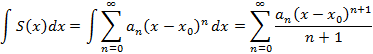
Полученные ряды также имеют интервал сходимости.
 2020-08-05
2020-08-05 1341
1341








