Пусть задана некоторая область D и в этой области задана непрерывная в заданной области функция 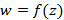 и некоторая кусочно-гладкая кривая
и некоторая кусочно-гладкая кривая 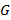
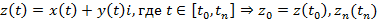
Разделив кривую на n произвольных частей, получим семейство дуг вида
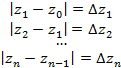
Исходя из этого получим следующее соотношение

Свойства интеграла комплексной переменной
1. Интеграл от алгебраической суммы равен алгебраической сумме интегралов. Справедливо для любого конечного числа слагаемых;
2. 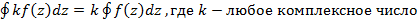 ;
;
3. 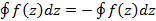 ;
;
4. 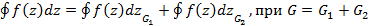
5. 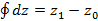 ;
;
6. 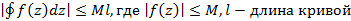 ;
;
Вычислить интеграл от комплексной переменной можно следующим образом
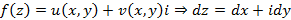
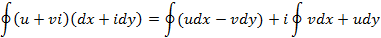
Полученное соотношение – контурный интеграл второго рода. Контурный интеграл первого рода, где 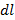 – дифференциал длины дуги имеет вид
– дифференциал длины дуги имеет вид
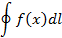
Интегральная теорема Коши для некоторой области
Если функция 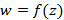 аналогична в заданной замкнутой односвязной области D, ограниченной контуром G, на котором она непрерывна, тогда получим соотношение, называемое условиями Коши-Римана
аналогична в заданной замкнутой односвязной области D, ограниченной контуром G, на котором она непрерывна, тогда получим соотношение, называемое условиями Коши-Римана
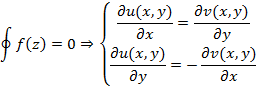
В условиях многосвязной области, которая может возникать в случае, когда функция комплексной переменной не аналогична в некоторой точке или области, ограниченной контуром 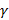 , интегральная теорема Коши представляется в виде суммы интегралов, рассматриваемых при односвязных областях
, интегральная теорема Коши представляется в виде суммы интегралов, рассматриваемых при односвязных областях
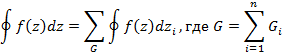
Исходя из этого соотношения получим для соотношение двусвязной области вида
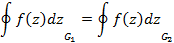
 2020-08-05
2020-08-05 119
119








