Пусть генеральная совокупность конечна и значения признака X распределены следующим образом 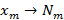 , где N – объем генеральной совокупности, тогда генеральной средней называется число
, где N – объем генеральной совокупности, тогда генеральной средней называется число
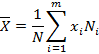
Генеральной дисперсией называется число

Если из генеральной совокупности случайным образом выбирается одна единица, тогда значение признака X на этой единице можно рассматривать как случайную величину с рядом распределения признак-вероятность  , тогда получим следующие соотношения для оценки среднего и дисперсии
, тогда получим следующие соотношения для оценки среднего и дисперсии
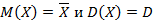
Данные выводы справедливы для и для бесконечных генеральных совокупностей.
Пусть по генеральной совокупности сделана выборка, преобразованная в дискретный вариационный ряд 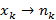 , где
, где  – объем выборки, тогда выборочное среднее и выборочная дисперсия будет равна
– объем выборки, тогда выборочное среднее и выборочная дисперсия будет равна
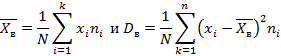
Выборочное среднее и выборочная дисперсия зависят от того, какие единицы попали в выборку, поэтому являются случайными величинами. Если выборка оформлена в интервальный вариационный ряд, тогда формулы числовых характеристик изменятся следующим образом
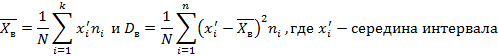
 2020-08-05
2020-08-05 100
100








