2020-08-05
87
Пусть признак X имеет некоторое распределение на генеральной совокупности с неизвестными параметрами. Пусть у рассматриваемой выборки существует параметр 
, тогда по данным выборки имеется возможность построить для него оценку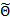 
, которая зависит от выборки и является случайной величиной.
Основные требования к точечным оценкам следующие
1. Состоятельность – при увеличении объема выборки оценка по вероятности должна стремится к истинному значению параметра
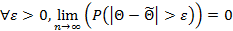
2. Несмещенность – при вычислении оценки мы не должны получать систематические ошибки в сторону занижения или увеличения истинного значения параметра;
3. Эффективность – при дискретном объеме выборки оценка должна иметь дисперсию, наименьшую из возможных.
Пусть параметр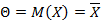 
, тогда в качестве оценки обычного рассматривают 
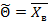, тогда она будет состоятельной исходя из теоремы Чебышева и несмещенной исходя из теоремы одинаково распределенных случайных величин и их средних арифметических.
В случае параметра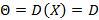 
, тогда в качестве оценки получим 
. Данная оценка будет состоятельной, смещенной со систематической ошибкой в сторону уменьшения. Для любого n оценка станет несмещенной, если взять исправленную выборочную дисперсию, где S – исправленная СКО
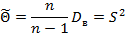
Такая оценка будет состоятельной, несмещенной и асимптотически эффективной для распределения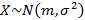 
– при фиксированном объеме выборки они будет давать наименьшую из возможных дисперсий.
