Пусть для параметра  признака X найдена точечная оценка. Необходимо оценить ошибку
признака X найдена точечная оценка. Необходимо оценить ошибку  . Поскольку ошибка является случайной величиной, тогда оценка может быть лишь вероятностной. Обозначим доверительную вероятность следующим соотношением, в котором
. Поскольку ошибка является случайной величиной, тогда оценка может быть лишь вероятностной. Обозначим доверительную вероятность следующим соотношением, в котором  – предельная ошибка выборки
– предельная ошибка выборки
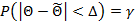
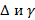 связанны между собой и зависят друг от друга
связанны между собой и зависят друг от друга
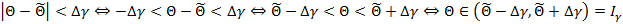
Полученное соотношение определяет доверительный интервал.
Если признак 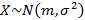 причем
причем  – известна, а m – неизвестна, тогда доверительный интервал для математического ожидания будет иметь вид
– известна, а m – неизвестна, тогда доверительный интервал для математического ожидания будет иметь вид
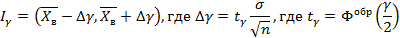
Данное соотношение справедливо в общем случае для нормально распределенных признаков с известным среднеквадратическим отклонением, но при больших объемах выборки  данную формулу можно использовать в случаях:
данную формулу можно использовать в случаях:
1. Если 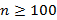 , тогда независимо от типа распределения признака X оценка среднего выборки находится на основе центральной предельной теоремы;
, тогда независимо от типа распределения признака X оценка среднего выборки находится на основе центральной предельной теоремы;
2. Если 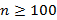 с неизвестным среднеквадратичным отклонением, тогда можно использовать соотношение для доверительного интервала, заменив среднеквадратическое отклонение на исправленное выборочное среднеквадратическое отклонение.
с неизвестным среднеквадратичным отклонением, тогда можно использовать соотношение для доверительного интервала, заменив среднеквадратическое отклонение на исправленное выборочное среднеквадратическое отклонение.
Пусть имеется случайная величина 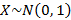 , тогда сумма неизвестных случайных величин
, тогда сумма неизвестных случайных величин 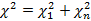 – случайная величина, распределенная по «хи-квадрат» c k степенями свободы. При стремлении к бесконечности данное распределение медленно сводится к нормальному распределению.
– случайная величина, распределенная по «хи-квадрат» c k степенями свободы. При стремлении к бесконечности данное распределение медленно сводится к нормальному распределению.
Пусть 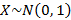 , тогда указанное соотношение случайной величины называется T-распределением или распределением Стьюдента
, тогда указанное соотношение случайной величины называется T-распределением или распределением Стьюдента
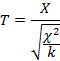
При стремлении степеней свободы распределения «хи-квадрат» к бесконечности данное распределение сводится к нормальному распределению.
Пусть 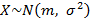 , где математическое ожидание и среднеквадратическое отклонение неизвестно, тогда значение математического ожидание с помощью доверительного интервала на основе Т-распределения
, где математическое ожидание и среднеквадратическое отклонение неизвестно, тогда значение математического ожидание с помощью доверительного интервала на основе Т-распределения
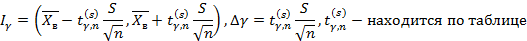
Оценка среднеквадратического отклонения находится на основе  -распределения
-распределения
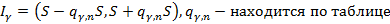
В данных соотношениях S – исправленное выборочное среднеквадратическое отклонение.
 2020-08-05
2020-08-05 119
119








