Тема 9. Дисконтирование и банковский учёт

"Даже если бы я был уверен в том, что вы уплатите моим наследникам 1 $ через 99 лет, то и в этом случае все равно я был бы глупцом, если бы дал вам сегодня больше 1 цента" Пол Самуэльсон.

 

Обратной операцией по отношению к начислению процентов является расчет современной стоимости будущих денег – дисконтирование.

В зависимости от того, какая ставка (процентная или учетная) применяется для дисконтирования, различают два его типа:

- математическое дисконтирование;

- банковский учёт.

При математическом дисконтировании используются простая и сложная процентные ставки. Расчеты выполняются по формулам:

С = Б / (1 + 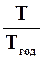К)                                    (22)

С = Б / (1 + К)^Т                                       (23)

Метод банковского учёта используется при осуществлении банками учётных операций с векселями.

Вексель – это ценная бумага установленной формы, содержащая безусловное денежное обязательство. Вексель является объектом купли-продажи, и его цена меняется в зависимости от изменения учетной ставки и оставшегося срока до платежа по векселю. На векселе указывается срок платежа, место платежа, наименование того, кому, или по приказу кого платеж должен быть совершен, указаны дата и место составления векселя, имеется подпись лица, выдавшего документ.

Простой вексель (соло-вексель) – это ничем не обусловленное бесспорное обещание должника уплатить определённую сумму по истечении срока векселя.

Переводной вексель (тратта) – это письменное требование уплатить определённую сумму. Выдача переводного векселя называется трассированием. Лицо, которое выписывает вексель – трассант; лицо, на которое выдан вексель, и которое должно произвести по нему платёж – трассат; лицо, на имя которого должник должен произвести платёж – ремитент.

Характерной деятельностью банков является учёт векселей. Владелец (простого или переводного) векселя может не ждать наступления срока платежа по векселю, а продать, а продать вексель банку, т.е. учесть вексель. Банк хранит вексель и при наступлении назначенного срока предъявляет его к платежу. За свою услугу банк удержит с продавца векселя определённый процент от вексельной суммы за её досрочное получение. Этот процент называется дисконт. Для определения цены и суммы дисконта используется учётная ставка.

Дисконт по учёту векселей рассчитывается по формуле:

Д = 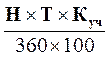                                      (24)

где: Н – номинал векселя;

Т – период в днях с момента принятия векселя к учёту до его погашения;

К_уч – учётная ставка банка (в процентах).

Цена, по которой векселедержатель продаёт вексель банку, определяется как разница между номиналом векселя и суммой дисконта.

 

Задание

1. Вексель номиналом 100000 руб. со сроком погашения 6 сентября учтен 3 июня при 9% годовых. Определите: сумму дисконта; дисконтированную стоимость векселя.

2. 10 апреля был учтен вексель со сроком погашения 9 июня. Найти номинал векселя, если учётная ставка банка 6% годовых, а векселедержатель получил 10 апреля 59400 руб.

3. Покупатель обязуется оплатить поставщику стоимость закупленных товаров через 90 дней после поставки в сумме 1000000 руб. Уровень простой процентной ставки составляет 30% годовых. При начислении используются обыкновенные проценты. Найти:

- текущую стоимость товаров методом математического дисконтирования;

- текущую стоимость товаров методом банковского учёта;

- определить, какой вариант является более выгодным для кредитора.

4. Тратта выдана на 10000000 руб. с уплатой 23 ноября. Владелец документа учёл его в банке 23 сентября. Учётная ставка равна 8% годовых. Найти сумму, которую выплатит банк при учёте векселя.

5. Через полгода заёмщик должен уплатить 1000000 руб. Ссуда выдана под 20% годовых. Найти, какую сумму получит заёмщик при заключении сделки

- при математическом дисконтировании;

- при банковском учёте.

6. Предприятие досрочно предъявило в банк к оплате купленный ранее дисконтный вексель этого банка. Срок платежа по векселю наступит через 10 дней. Номинал векселя равен 50 млн. руб. Учётная ставка – 16% годовых. Требуется:

- рассчитать сумму дисконта по векселю;

- определить сумму, которую банк заплатит по векселю.

Тема 10. Начисление банковских процентов
в условиях инфляции

"Инфляция является самым жестоким налогом из всех существующих"

На размер процентных ставок коммерческих банков большое влияние оказывает уровень инфляции, приводящий к обесцениванию денежных доходов. Если рост инфляции выше роста доходов вкладчиков, определяемых предлагаемыми банком процентными ставками, вкладчики могут выбрать более доходный источник инвестирования своих временно свободных денежных средств. При количественной оценке инфляции используют два показателя – уровень и индекс инфляции.

Уровень инфляции (U_Т) показывает, на сколько процентов выросли цены за рассматриваемый период времени. Индекс инфляции (I_Т) показывает, во сколько раз выросли цены за этот же период времени. Индекс можно выразить следующим образом:

I _Т = (1 + U _Т )^T,                                          (25)

где: Т – анализируемый период в месяцах.

Тогда реальное значение будущей суммы с учетом инфляции за рассматриваемый срок определяется:

Б_р = Б / I _Т ,                                                (26)

где: Б_р – реальное значение полученной суммы вкладчиком с учетом её покупательной способности;

Б – сумма, выданная банком клиенту в день закрытия депозитного счета;

I_Т – индекс инфляции за период Т.

 

Задание

1. Среднемесячный уровень инфляции составляет 7%. Найти индекс инфляции за год.

2. Вклад в сумме 80000 рублей внесен в банк на полгода с ежемесячным начислением сложных процентов по годовой ставке 120%. Средний уровень инфляции составил 10% в месяц. Найти реальный доход вкладчика с точки зрения его покупательной способности.

3. На взносы на депозитный счет, вносимые в конце каждого квартала по полугодиям будут начисляться сложные проценты по ставке 19% годовых. Размер квартальных взносов 3000 руб. Найти реальное значение полученной суммы с учетом инфляции, если уровень инфляции 1,5% в месяц. Срок хранения вклада 1 год.

4. По полугодиям начисляются сложные проценты по ставке 43% годовых. Найти размер квартальных взносов, если будет накоплено через год 5000 рублей. Учесть, что суммы вносятся в конце квартала. Рассчитать реальное значение полученной суммы, если уровень инфляции в среднем составил 4,5% в месяц.

5. В сбербанк клиент внес 10000 рублей под 14% годовых. Ожидаемый ежемесячный уровень инфляции в 2003 г. 1,8%. Найти, обеспечивает ли банк сохранность средств вкладчика.

6. Вкладчик внёс в Сбербанк 1 июля 2000 года 15000 руб. на полгода. Банк обещает начислить проценты по ставке 16% годовых. Найти реальный доход вкладчика с учётом инфляции, если в федеральном бюджете на 2000 год запланирован средний уровень инфляции 1,5% в месяц. Банк предлагает следующие варианты начисления:

- простые проценты;

- сложные проценты;

- ежеквартальное начисление сложных процентов.

7. При открытии счета до востребования 10.09.00 г. была внесена сумма 1800 руб. под 3% годовых; 15.10.00 г. было добавлено ещё 600 руб.; 30.10.00 г. ещё плюс 1500 руб.; 30.11.00 вкладчик снял 850 руб.; 15.12.00 г. добавил 1000 руб. Счет был закрыт 08.01.01 г. Среднемесячный уровень инфляции за период действия депозитного договора 12%. Найти реальный доход вкладчика.

8. Вклад в сумме 500000 руб. положен в банк на 2 года с ежеквартальным начислением сложных процентов по номинальной годовой ставке 10%. Определить реальный доход вкладчика для ожидаемого месячного уровня инфляции 1,5% и 2%.