Цель: сформировать умение решать логарифмические уравнения и неравенства
Теоретические сведения к практическому занятию:
При решении логарифмических уравнений и неравенств используются следующие утверждения:
1) если 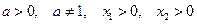 , то равенство
, то равенство 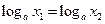 справедливо тогда и только тогда, когда
справедливо тогда и только тогда, когда 
2) если 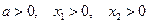 , то неравенство
, то неравенство 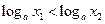 справедливо тогда и только тогда, когда
справедливо тогда и только тогда, когда 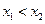
3) если 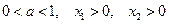 , то неравенство
, то неравенство 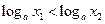 справедливо тогда и только тогда, когда
справедливо тогда и только тогда, когда 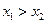
Простейшие логарифмические неравенства  , где
, где 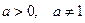 , имеют решения при любом
, имеют решения при любом 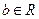 .
.
Если 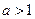 , то множество решений неравенства (*) – промежуток
, то множество решений неравенства (*) – промежуток 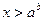 , а множество решений неравенства (**) – интервал
, а множество решений неравенства (**) – интервал 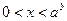 .
.
Если 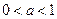 , то множество решений неравенства (*) – интервал
, то множество решений неравенства (*) – интервал 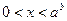 , а множество решений неравенства (**) – промежуток
, а множество решений неравенства (**) – промежуток 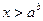 .
.
Неравенство 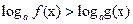 при
при 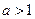 равносильно двойному неравенству
равносильно двойному неравенству 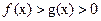 , а при
, а при 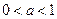 - двойному неравенству
- двойному неравенству 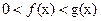 .
.
Пример: Решить уравнения
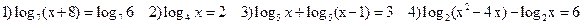 Решение:
Решение:
19
Пример: Решить неравенства
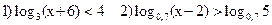
Решение:
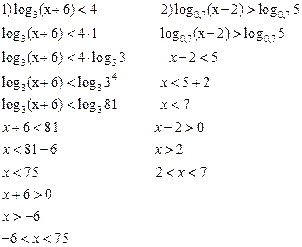
Самостоятельная работа:
1) Решить уравнения:
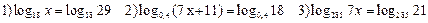
2) Решить неравенства:
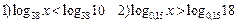
Содержание практического занятия:
А. Ответить на вопросы:
1) Какие свойства логарифмической функции используются при решении логарифмических уравнений и неравенств?
3) Приведите примеры логарифмических уравнений с решениями.
Б. Выполнить задания:
1) Решить уравнения:
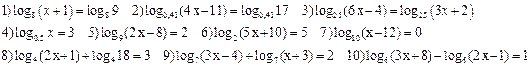
2) Решить неравенства:
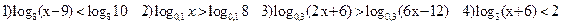
Тема: «Системы показательных и логарифмических уравнений и неравенств»
Цель: сформировать умение решать системы показательных и логарифмических уравнений и неравенств
Теоретические сведения к практическому занятию:
Пример: Решить систему уравнений
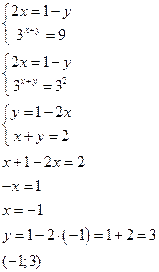
Пример: Решить систему
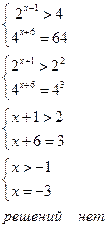
Пример: Решить систему
22

Самостоятельная работа:
1) Решить системы:
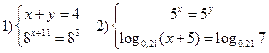
2) Решить системы:
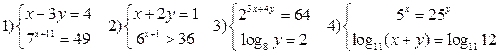
 2020-09-24
2020-09-24 101
101








