2020-09-24
148
Если 
, тогда справедливы 3 утверждения:
1. 
, причем замкнутый контур к полностью находится внутри области D.
2. 
не зависит от формы кривой АВ, если и сама кривая, и точки АВ полностью находятся в области D, а зависит только от положения точек АВ.
3. Если подынтегральное выражение является полным дифференциалом 
, тогда можно восстановить саму функцию.
, с – произвольная постоянная.
Примеры.
Рассмотрим 2-ое следствие.
Вычислить 
где кривая L соединяет точки О и А.
L: O(0;0), A(
).
P=x+y; 
; Q=x-y; 
.
1)Пусть L – прямая ОА.
ОА: y=x, 
, 
.
.
2) Пусть кривая L –ломанная ОАВ, В(π;0).
ОВ: y=0, 
.
.
BA: x=π, 
.
.
.
3) Пусть кривая L – парабола OA: 
Рассмотрим третье следствие.
Восстановить функцию 
.
; 
. 
; 
.
M0(1;1), M(X;Y)
1) 
.
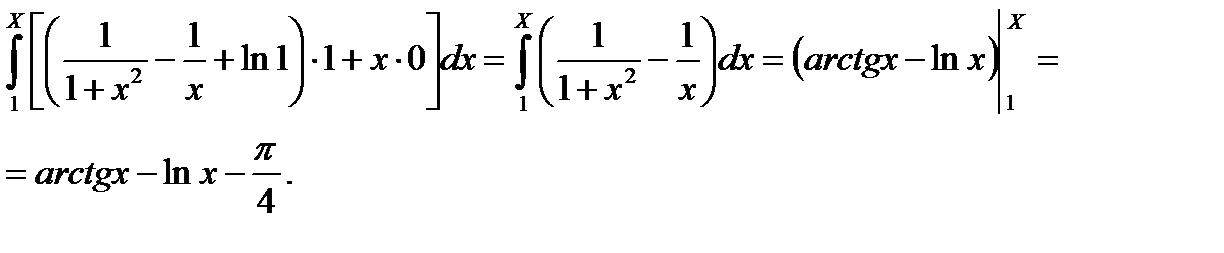
2) 
.
.
;
Пусть 
.
.
Применение криволинейного интеграла 2-го рода.
1) Вычисление работы по перемещению точки вдоль кривой L под действием силы 
.
.
2) Вычисление площади плоской фигуры, ограниченной замкнутой линией L
.
Пример. Вычислить площадь фигуры, ограниченной линиями 
.
, P=-y, Q=x.
1) 
.
.
2) 
.
.
3) 
.
.
.
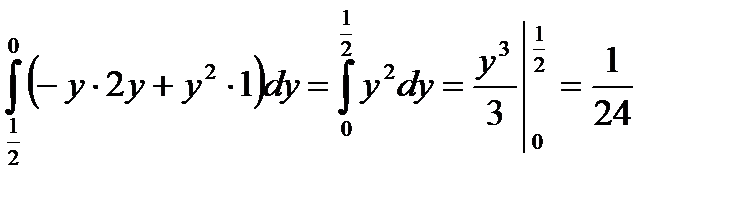Пример. Вычислить работу силы 
при перемещении точки по контуру эллипса 
, лежащего в 1-ой четверти.
.
АВ: Запишем параметрически уравнение эллипса:
, 
. 
.
