2020-09-24
193
1) монотонные функции;
2) ограниченные и неограниченные функции;
3) чётные и нечётные функции;
4) периодические функции.
1) монотонные функции:
Определение 1. Функция 
называется возрастающей на множестве 
, если для любых 
из условия 
следует 
.
Определение 2. Функция называется убывающей на множестве , если для любых из условия следует 
.
Возрастающие и убывающие функции называются строго монотонными.
Определение 3. Функция называется неубывающей на множестве , если для любых 
из условия 
следует 
.
Определение 4. Функция называется невозрастающей на множестве , если для любых из условия следует 
.
Функции всех четырёх классов называются монотонными.
Определение 5. Функция называется кусочно-монотонной, если её область определения 
можно разбить на конечное множество промежутков, на каждом из которых функция монотонна.
Примеры: 
, 
2) ограниченные и неограниченные функции:
Определение 1. Функция называется ограниченной сверху на множестве , если множество 
является ограниченным сверху, то есть 
.
Определение 2. Функция называется ограниченной снизу на множестве , если множество является ограниченным снизу, то есть 
.
Определение 3. Функция называется ограниченной на множестве , если множество ограничено, то есть 
.
В противном случае функция называется неограниченной.
3) чётные и нечётные функции:
Определение 1. Функция называется чётной, если:
1) симметрична относительно начала координат, то есть если 
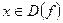, то 
;
2) 
.
Определение 2. Функция называется нечётной, если:
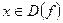1) симметрична относительно начала координат, то есть если , то ;
2) 
.
4) периодические функции:
Определение. Функция называется периодической с периодом 
, если:
1) 
;
2) 
.
Если 
– период функции 
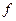, то для любого 
- тоже период. Наибольшего периода не существует. Но не всякая функция имеет наименьший положительный период.
Пример:
Функция Дирихле не имеет наименьшего положительного периода, так как 
, отсюда любое 
есть период функции 
, но наименьшего положительного рационального числа не существует.
