2020-09-24
93
Определение 1. Последовательность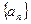 
называется ограниченной, если существует такое положительное число M, что для любого 
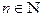выполняется неравенство 
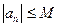(то есть 
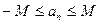). В противном случае последовательность называется неограниченной.
Примеры:
1) 
.
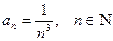Последовательность имеет вид: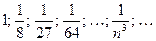 
.
Так как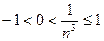 
, то 
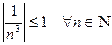. Тогда по определению 1 последовательность 
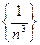ограничена.
2) 
.
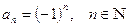Последовательность имеет вид: -1; 1; -1; 1; -1; 1; …;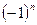 
; ….
Так как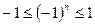 
, то 
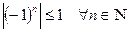. Тогда по определению 1 последовательность 
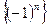ограничена.
Определение 2. Последовательность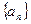 
называется возрастающей, если для любого 
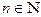выполняется неравенство 
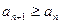. Если же 
, то последовательность 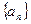называется строго возрастающей.
Определение 3. Последовательность 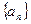называется убывающей, если для любого 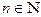имеет место неравенство 
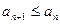. Если же 
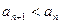, то последовательность 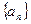называется строго убывающей.
Все эти последовательности называются монотонными последовательностями.
Пример: Последовательность задана формулой 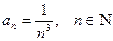. Тогда 
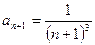. Так как 
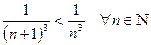, т.е. 
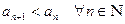, то последовательность 
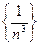строго убывает.
|
|
|
