ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Определение. Бесконечной числовой последовательностью называется числовая функция 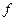 , определённая на множестве всех натуральных чисел
, определённая на множестве всех натуральных чисел 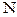 . Её обозначают
. Её обозначают 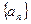 или
или 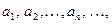 где
где 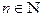 .
.
Число 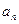 называется n – м (общим) членом последовательности, а число n – номером члена
называется n – м (общим) членом последовательности, а число n – номером члена 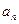 .
.
Способы задания числовой последовательности:
1. Задание функции 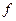 , порождающей последовательность:
, порождающей последовательность:
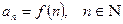 (1)
(1)
Формулу (1) называют формулой общего члена последовательности. По этой формуле можно вычислить любой член последовательности.
Примеры:
1) 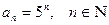 .
.
Тогда 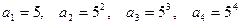 и т.д.
и т.д.
Последовательность имеет вид: 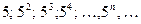 .
.
2) 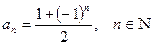 .
.
Тогда 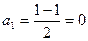 ,
, 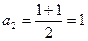 ,
, 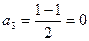 ,
, 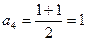 и т.д.
и т.д.
Последовательность имеет вид: 0; 1; 0; 1; 0; 1; 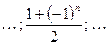 .
.
Последовательность, у которой все члены принимают равные между собой значения, называется постоянной последовательностью.
2. Рекуррентный способ задания последовательности, который состоит в том, что указывается правило, позволяющее вычислить общий член последовательности через предыдущие члены, а также задаются несколько начальных членов последовательности. Формула, позволяющая вычислить общий член последовательности через предыдущие члены, называется рекуррентным соотношением.
Пример: 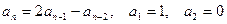 .
.
Тогда 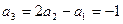 ;
;
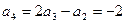 ;
;
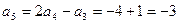 ;
;
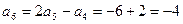 ;
;
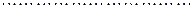
Последовательность имеет вид: 1; 0; -1; -2; -3; -4;….
3. Последовательность задаётся словесно, то есть описанием её членов.
 2020-09-24
2020-09-24 107
107








