Математический анализ
Тула
ТППО
2019
ББК: 74.489
И85
Рецензент:
кандидат физико-математических наук, доцент О. А. Пихтилькова
(Оренбургский государственный университет);
кандидат физико-математических наук, доцент В.В.Носов
(Оренбургский государственный университет);
| Р60 | Математический анализ/ Сост. Н.М. Исаева, Н.В.Мыслик, Е.М. Рарова, О. В. Родионова, Л.Д. Ситникова, Н.В. Сорокина. – Тула: ТППО, 2019. – 75 с. |
| Настоящее пособие предназначено студентам педвузов, обучающимся по направлению 44.03.01 Педагогическое образование (профиль «Информатика») для изучения дисциплины «Математический анализ» и по направлению 44.03.01 Педагогическое образование (профиль «Математика») при изучении дисциплин «Введение в математический анализ», «Дифференциальное исчисление» и «Интегралы и ряды». Пособие может использоваться при изучении дисциплины «Теория функций одной переменной» студентами, обучающимися по направлению 44.03.05 Педагогическое образование (профили «Физика» и «Математика», «Физика» и «Астрономия). В пособии подробно рассмотрены такие разделы, как введение в анализ, дифференциальное исчисление функции одной переменной, а также неопределённый интеграл и определённый интеграл. Приведены примеры, варианты самостоятельных работ, дополнительные задания по перечисленным разделам. |
ББК 74.489
Учебно-методическое пособие
Математический анализ
Составители:
Исаева Нина Магомедрасуловна
МЫСЛИК Надежда Владимировна
РАРОВА Елена Михайловна
РОДИОНОВА Ольга Владимировна
СИТНИКОВА Людмила Дмитриевна
СОРОКИНА Наталия Владимировна
Печатается с авторского оригинал-макета.
Подписано в печать 24.11.2019. Формат 60´90/16.
Бумага офсетная. Печать трафаретная.
Усл. печ. л. 5. Уч.-изд. л. 5,95. Тираж 100 экз.
ООО «Тульское производственное полиграфическое объединение».
300600, Тула, ул. Каминского, 33.
| © | Сост.: Н.М. Исаева, Н.В.Мыслик, Е.М. Рарова, О. В. Родионова, Л.Д. Ситникова, Н.В. Сорокина, 2019 |
СОДЕРЖАНИЕ
| РАЗДЕЛ 1. | ВВЕДЕНИЕ В АНАЛИЗ | 44 |
| тема 1. | ФУНКЦИЯ | 44 |
| тема 2. | ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ | 57 |
| тема 3. | ПРЕДЕЛ ФУНКЦИИ | 65 |
| тема 4. | СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ. ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ | 68 |
| тема 5. | НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ | 72 |
| РАЗДЕЛ 2. | ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ | 2 |
| тема 6. | ПРОИЗВОДНАЯ ФУНКЦИИ. ГЕОМЕТРИЧЕСКИЙ И МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ | 2 |
| тема 7. | ДИФФЕРЕНЦИАЛ ФУНКЦИИ. ПРОИЗВОДНЫЕ РАЗЛИЧНЫХ ПОРЯДКОВ | 7 |
| тема 8. | ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ | 11 |
| тема 9. | ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ ПРОИЗВОДНОЙ | 15 |
| РАЗДЕЛ 3. | НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ | 23 |
| тема 10. | ОПРЕДЕЛЕНИЕ И СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА | 23 |
| тема 11. | ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ | 27 |
| тема 12. | ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ И ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ | 31 |
| РАЗДЕЛ 4. | ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ | 34 |
| тема 13. | ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА | 34 |
| тема 14. | ВЫЧИСЛЕНИЕ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ | 39 |
| тема 15. | ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА | 43 |
| РАЗДЕЛ 5. | варианты контрольных работ | 49 |
| СПИСОК ЛИТЕРАТУРЫ | 51 | |
РАЗДЕЛ 1. ВВЕДЕНИЕ В АНАЛИЗ
Тема 1. ФУНКЦИЯ
Определение 1. Функцией (или отображением) из множества X в множество Y будем называть правило f, по которому каждому элементу из множества X соответствует единственный элемент из множества Y. 
Элемент 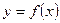 называется образом элемента x при отображении f.
называется образом элемента x при отображении f.
Определение 2. Если 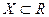 ,
, 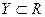 , то функцию f называют действительной функцией действительной переменной.
, то функцию f называют действительной функцией действительной переменной.
Множество 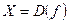 называют областью определения функции f, множество
называют областью определения функции f, множество 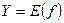 называют множеством значений функции f,
называют множеством значений функции f, 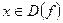 называют аргументом функции f, а
называют аргументом функции f, а 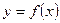 – значением функции f в точке x (
– значением функции f в точке x (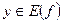 ).
).
СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ
1) аналитический;
2) графический;
3) табличный;
4) описательный.
1) аналитический способ: наиболее часто функцию задают с помощью формулы (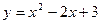 ,
, 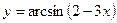 ). Под областью определения в этом случае естественно понимать множество всех значений x, для которых определено значение выражения
). Под областью определения в этом случае естественно понимать множество всех значений x, для которых определено значение выражения 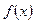 .
.
Пример:
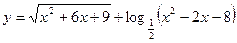
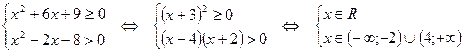
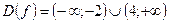
2) графический способ:
Определение. Графиком функции 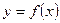 называется множество
называется множество 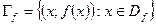 точек координатной плоскости.
точек координатной плоскости.
Замечание. Некоторое множество координатной плоскости является графиком некоторой функции, если это множество имеет не более одной общей точки с любой прямой, параллельной оси OY.
Наиболее важными при рассмотрении графика функции являются две задачи:
1) функция f задана аналитически. Требуется исследовать свойства этой функции и построить её график (часто это эскиз графика).
Пример:
1) 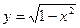 – можно построить график точно;
– можно построить график точно;
2) 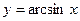 – можно построить эскиз графика.
– можно построить эскиз графика.
2) функция f задана графически. Требуется определить основные свойства функции, т.е. «прочитать» график.
3) табличный способ:
| x | 1 | 2 | 3 | 4 | 
|
| y | 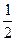
| 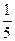
| 1 | 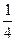
| 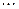
|
4) описательный способ:
В случаях, когда формулу, по которой каждому 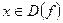 ставится в соответствие
ставится в соответствие 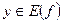 , записать трудно (или невозможно), пользуются словесным описанием способа, задающего функцию.
, записать трудно (или невозможно), пользуются словесным описанием способа, задающего функцию.
Пример:
Каждому действительному числу x ставится в соответствие наибольшее целое число, не превосходящее x. Эта функция называется целой частью x и обозначается 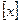 .
.
 2020-09-24
2020-09-24 181
181







