Определение. Последовательность называется бесконечно малой, если её предел равен нулю.
Пример: 
Последовательность 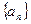 имеет вид:
имеет вид: 
Покажем, что  .
.
Зафиксируем  и найдём N, такое, что
и найдём N, такое, что  из условия
из условия 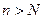 следует
следует  , отсюда
, отсюда 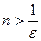 и
и  . Таким образом,
. Таким образом,  и последовательность
и последовательность  является бесконечно малой последовательностью.
является бесконечно малой последовательностью.
Теорема 1. Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Доказательство:
Пусть 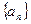 и
и  – бесконечно малые последовательности. Тогда
– бесконечно малые последовательности. Тогда


 ,
,


 .
.
Выбираем  . Тогда для любого
. Тогда для любого 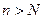 справедливы неравенства
справедливы неравенства
 , т.е.
, т.е.
 . (3)
. (3)
Так как  взято произвольным, из неравенства (3) следует, что
взято произвольным, из неравенства (3) следует, что  . Таким образом, последовательность
. Таким образом, последовательность  является бесконечно малой.
является бесконечно малой.
Теорема 2. Произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.
Доказательство:
Пусть  – ограниченная последовательность. Тогда
– ограниченная последовательность. Тогда
 (4)
(4)
Пусть 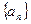 – бесконечно малая последовательность. Тогда
– бесконечно малая последовательность. Тогда
 (5)
(5)
Из условий (4) и (5) следует, что

для любого  при условии
при условии  . Отсюда
. Отсюда  , т.е. последовательность
, т.е. последовательность  бесконечно малая.
бесконечно малая.
Пример:

 - бесконечно малая последовательность;
- бесконечно малая последовательность;
 - ограниченная последовательность, так как
- ограниченная последовательность, так как  .
.
Отсюда  - бесконечно малая последовательность и
- бесконечно малая последовательность и  .
.
Теорема 3. Для того чтобы число a было пределом последовательности 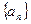 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы  могло быть представлено в виде
могло быть представлено в виде  , где
, где  – бесконечно малая последовательность, т.е.
– бесконечно малая последовательность, т.е. 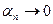 при
при 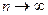 .
.
Доказательство:
1) Необходимость.


 .
.
Обозначим  и получим
и получим
 .
.
Тогда  , отсюда
, отсюда  – бесконечно малая последовательность и
– бесконечно малая последовательность и  .
.
2) Достаточность.
Пусть  и
и  . Тогда
. Тогда
 .
.
Так как  , получаем
, получаем  . Следовательно,
. Следовательно, 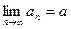 .
.
 2020-09-24
2020-09-24 161
161








