Теорема 1 (о пределе суммы). Если последовательности 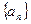 и
и 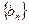 сходятся, то их сумма
сходятся, то их сумма 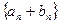 тоже сходится и предел суммы равен сумме пределов:
тоже сходится и предел суммы равен сумме пределов:
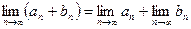 .
.
Доказательство:
Пусть 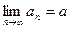 ,
, 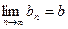 . Тогда по рассмотренной в предыдущем пункте теореме 3 имеем
. Тогда по рассмотренной в предыдущем пункте теореме 3 имеем
 ,
, 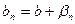
где 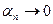 и
и 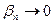 при
при 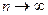 . Следовательно,
. Следовательно,
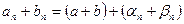 ,
,
где 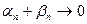 при
при 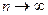 , так как сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность. Тогда по теореме 3 получаем:
, так как сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность. Тогда по теореме 3 получаем:
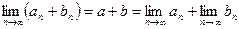 .
.
Теорема 2 (о пределе произведения). Если последовательности 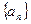 и
и 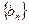 сходятся, то их произведение
сходятся, то их произведение 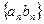 сходится и предел произведения равен произведению пределов:
сходится и предел произведения равен произведению пределов:
 .
.
Доказательство: Пусть 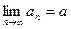 ,
, 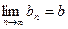 . Тогда по рассмотренной в предыдущем пункте теореме 3 имеем
. Тогда по рассмотренной в предыдущем пункте теореме 3 имеем
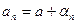 ,
, 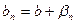
где 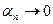 и
и 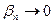 при
при 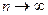 . Следовательно,
. Следовательно,
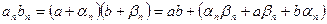 ,
,
где 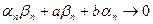 при
при 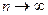 (по теоремам 1 и 2 предыдущего пункта). Тогда по теореме 3 получаем:
(по теоремам 1 и 2 предыдущего пункта). Тогда по теореме 3 получаем:
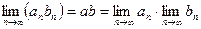 .
.
Следствие 1. Постоянный множитель можно выносить за знак предела:
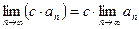 .
.
Доказательство: Пусть 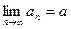 ,
, 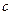 - постоянная, следовательно,
- постоянная, следовательно,  . Тогда по теореме о пределе произведения получаем:
. Тогда по теореме о пределе произведения получаем:
 .
.
Следствие 2. Если последовательности 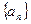 и
и 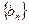 сходятся, то их разность
сходятся, то их разность 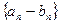 тоже сходится и предел разности равен разности пределов:
тоже сходится и предел разности равен разности пределов:
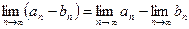 .
.
Доказательство: самостоятельно.
Теорема 3 (о пределе частного). Если последовательности 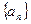 и
и 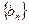 сходятся, причём
сходятся, причём 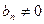 и
и 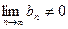 , то их частное
, то их частное 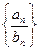 тоже сходится и предел частного равен частному пределов:
тоже сходится и предел частного равен частному пределов:
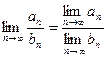 .
.
Доказательство: Пусть 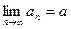 ,
, 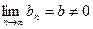 . Тогда
. Тогда 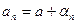 ,
, 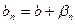 , где
, где  и
и 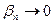 при
при 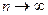 . Следовательно,
. Следовательно,
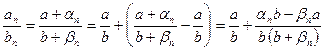 ,
,
где 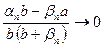 при
при 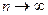 (по теоремам 1 и 2 предыдущего пункта). Тогда по теореме 3 получаем:
(по теоремам 1 и 2 предыдущего пункта). Тогда по теореме 3 получаем:
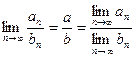 .
.
Примеры:
1) 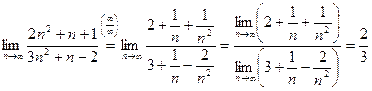
2) 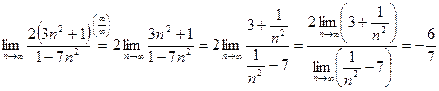
 2020-09-24
2020-09-24 206
206








