Определение. Последовательность 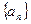 называется бесконечно большой, если для любого
называется бесконечно большой, если для любого 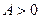 найдётся такой номер
найдётся такой номер 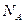 , что для всех
, что для всех 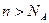 верно неравенство
верно неравенство  . В этом случае пишут
. В этом случае пишут  .
.
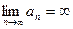

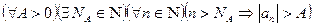
Теорема. Если последовательность 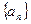 , где
, где 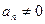 , бесконечно большая, то последовательность
, бесконечно большая, то последовательность 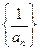 бесконечно малая. Верно обратное утверждение: если последовательность
бесконечно малая. Верно обратное утверждение: если последовательность 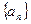 бесконечно малая, то последовательность
бесконечно малая, то последовательность 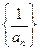 бесконечно большая.
бесконечно большая.
Доказательство:
1) 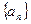 – бесконечно большая последовательность, тогда
– бесконечно большая последовательность, тогда
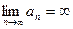

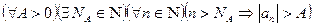 .
.
Зафиксируем 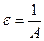 :
:

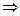
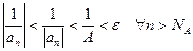 ,
,
Следовательно, 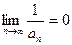 , т.е. последовательность
, т.е. последовательность 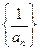 – бесконечно малая.
– бесконечно малая.
2) 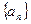 - бесконечно малая последовательность, тогда
- бесконечно малая последовательность, тогда
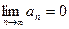

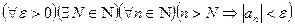
Положим 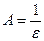 :
:
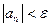
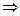
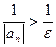 .
.
Таким образом,  для любого
для любого 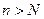 . Отсюда
. Отсюда 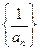 – бесконечно большая последовательность.
– бесконечно большая последовательность.
Пример:

Последовательность 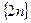 – бесконечно большая, тогда последовательность
– бесконечно большая, тогда последовательность 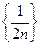 – бесконечно малая и
– бесконечно малая и 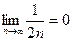 .
.
 2020-09-24
2020-09-24 137
137








