Тема 3. Предел функции

Определение 1. Пусть функция 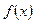определена в некоторой окрестности точки a, кроме, может быть, самой точки a. Число A называется пределом функции 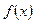в точке a (или при x, стремящемся к a), если для любой последовательности допустимых значений аргумента , сходящейся к a (т.е. ), последовательность соответствующих значений функции сходится к числу A. В этом случае пишут или при .

Определение 2. Назовём окрестностью точки c любой интервал , содержащий c, а – окрестностью точки c интервал , где .

Определение 3. Число A называется пределом функции 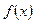при стремлении x к a (или в точке a), если для любого числа существует такое число , что для всех , удовлетворяющих условию , имеет место неравенство .

Обозначение: или при .

Графическая иллюстрация.

Так как из неравенства следует неравенство , то это означает, что для всех точек x, отстоящих от точки a не далее чем на , точки графика функции лежат внутри полосы шириной , ограниченной прямыми и .

Примеры:

1) Доказать, что .

Фиксируем , покажем, что , такое, что для из условия следует .Очевидно, .

2) Доказать, что .

Фиксируем , покажем, что , такое, что для всех из условия следует .

тогда , отсюда .

Найдём : .

Определение 4. Число A называется пределом функции 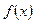при стремлении x к бесконечности, если для любого числа существует такое положительное число N, что для всех x, удовлетворяющих условию имеет место неравенство . При этом пишут .

Предел функции 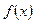при () определяется аналогично пределу функции при 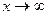, только в самой формулировке определения предела функци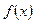и при 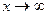условие следует заменить на ().