Односторонние пределы

 

Если при нахождении предела рассматривать значения x только слева от точки a, то такой предел называется левым или левосторонним и обозначается

.

а если рассматривать значения x только справа от точки a, то такой предел называется правым или правосторонним и обозначается

.

Из этих определений следует, что если существует предел

,                                          (1)

то существуют и односторонние пределы, причём

.                                  (2)

Верно и обратное утверждение: если имеет место (2), то имеет место и (1).

Пример:

Найти односторонние пределы функции   в точке . Существует ли у этой функции предел при ?

;

;

 - не существует.

 

НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ.

СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ В ТОЧКЕ

 

Определение 1. Функция 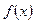 называется непрерывной в точке , если она задана в этой точке и в некоторой её окрестности и если .

Пример:

Функция  непрерывна в любой точке  и поэтому , например, .

Согласно данному определению, непрерывность функции 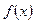 в точке  означает одновременную выполнимость следующих условий:

1) функция 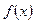 должна быть задана в точке  и в некоторой её окрестности;

2) существуют  и ;

3) ;

4) .

Если хотя бы одно из условий 1) - 4) не выполняется, то функция  будет разрывной в точке , а точка  называется точкой разрыва функции .