Определение 1. Пусть функции 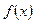 и
и  бесконечно малые при
бесконечно малые при 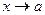 .
.
Если  , то
, то 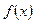 бесконечно малая более высокого порядка малости, чем
бесконечно малая более высокого порядка малости, чем  .
.
Если  , то
, то 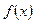 и
и  – бесконечно малые одного порядка малости.
– бесконечно малые одного порядка малости.
Если  ,то
,то 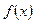 бесконечно малая более низкого порядка малости, чем
бесконечно малая более низкого порядка малости, чем  .
.
Если  не существует, то
не существует, то 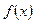 и
и  несравнимые бесконечно малые.
несравнимые бесконечно малые.
Примеры:
1) 
2) 
3)  (вследствие примера 1)
(вследствие примера 1)
4)  - не существует
- не существует
Определение 2. Функцию  при
при 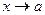 называют функцией первого порядка малости;
называют функцией первого порядка малости;
функцию  при
при 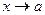 называют функцией второго порядка малости;
называют функцией второго порядка малости;







функцию  при
при 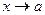 называют функцией n - го порядка малости.
называют функцией n - го порядка малости.
Определение 3. Если  , где
, где 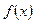 ,
,  бесконечно малые при
бесконечно малые при 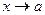 , то
, то  и
и  называются эквивалентными бесконечно малыми при
называются эквивалентными бесконечно малыми при 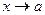 .
.
(обозначение  ~
~  )
)
Теорема. Пусть функции  ,
,  ,
,  ,
,  бесконечно малые при
бесконечно малые при 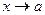 . При этом
. При этом  ~
~  ,
,  ~
~  при
при 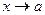 и
и  . Тогда
. Тогда  .
.
Доказательство:

ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
Пределы  и
и  принято называть первым и вторым замечательными пределами ввиду их важности в дальнейших приложениях.
принято называть первым и вторым замечательными пределами ввиду их важности в дальнейших приложениях.
Теорема 1. Предел  существует и равен единице.
существует и равен единице.


 ~
~  при
при 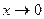
Доказательство:
Рассмотрим единичную окружность, пусть  - угол (
- угол ( ).
).
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Получаем неравенство  , т.е.
, т.е.  .
.
Поделим последнее неравенство на 
 :
:
 .
.

Отсюда следует
 . (*)
. (*)
Так как  и
и  – чётные функции, то неравенство (*) выполняется для
– чётные функции, то неравенство (*) выполняется для  , т.е. (*) имеет место в проколотой окрестности
, т.е. (*) имеет место в проколотой окрестности  .
.
Так как  ,
,  и выполняется (*), то
и выполняется (*), то  (по теореме о пределе промежуточной функции).
(по теореме о пределе промежуточной функции).
Примеры:
1) 

 ~
~  при
при 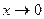
2) 

 ~
~  при
при 
 ~
~  при
при 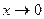
 ~
~  при
при 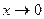
3) 

 ~
~  при
при 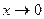
замена:  ,
,  ,
, 
4) 

 ~
~  при
при 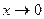
замена:  ,
,  ,
, 
ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
Теорема. Функция  стремится при
стремится при  к пределу e:
к пределу e:
 (неопределённость
(неопределённость  ).
).
Обозначим  ,
,  . Тогда
. Тогда
 .
.
Таким образом,  .
.
Некоторые примеры пределов функций.
1) 
Доказательство:

Следствие 1. Пусть  , тогда
, тогда  , т.е.
, т.е.  ~
~  при
при  .
.
2) 
Доказательство:

 , замена:
, замена:  ,
, 

Следствие 2. Пусть  , тогда
, тогда  , т.е.
, т.е.  ~
~  при
при  .
.
3) 
Доказательство:

 ,
,
 ,
,

По следствию 1  ~
~ 
 при
при  .
.
Следствие 3.  , т.е.
, т.е.  ~
~  при
при  .
.
Тема 5. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ
 2020-09-24
2020-09-24 389
389








