Определение производной. Пусть задана функция 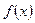 ,
, 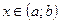 и пусть
и пусть 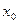 - некоторая точка интервала
- некоторая точка интервала 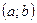 . Предел
. Предел
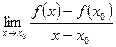
называется производной функции 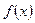 в точке
в точке 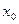 и обозначается
и обозначается 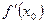 (если последний предел существует). Таким образом, по определению,
(если последний предел существует). Таким образом, по определению,
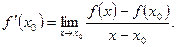
Функция, имеющая производную в некоторой точке, называется дифференцируемой в этой точке. Функция  ,
,  , имеющая в каждой точке интервала
, имеющая в каждой точке интервала 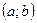 производную, называется дифференцируемой на этом интервале. Операция нахождения производной данной функции называется дифференцированием.
производную, называется дифференцируемой на этом интервале. Операция нахождения производной данной функции называется дифференцированием.
Обозначение производной функции 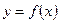 :
: 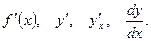
Если ввести приращение аргумента 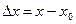 и приращение функции
и приращение функции 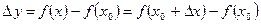 , определение производной запишется в виде
, определение производной запишется в виде
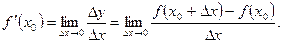
Так как 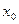 - произвольное значение аргумента, то можно обозначить его как x. Тогда получаем
- произвольное значение аргумента, то можно обозначить его как x. Тогда получаем
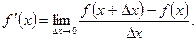
Примеры:
1) Дана функция 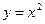 , найдите её производную.
, найдите её производную.
Решение.
а) 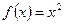 ,
, 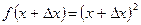 ,
,
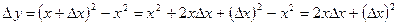
б) 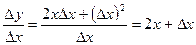
в) 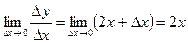
Таким образом, 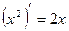 .
.
2) Найдите производную функции 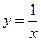 .
.
Решение.
а) 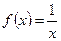 ,
, 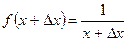 ,
,
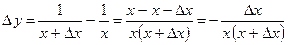
б) 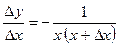
в) 
Непрерывность дифференцируемой функции
Докажем необходимое условие существования производной.
Теорема. Если функция 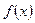 имеет производную в точке
имеет производную в точке 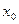 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Доказательство: По определению производной 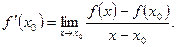
Тогда по свойству предела функции получаем 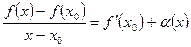 , где
, где  . Отсюда
. Отсюда
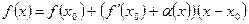 .
.
Находим предел функции 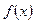 при
при 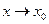 :
:
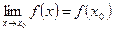 .
.
Отсюда по определению функция 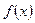 непрерывна в точке
непрерывна в точке 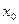 .
.
Замечания: 1) В точках разрыва функция не имеет производной.
2) Непрерывность функции в точке не является достаточным условием существования производной этой функции в рассматриваемой точке, т.е. из непрерывности функции в точке не следует её дифференцируемость в этой точке.
Пример: Пусть 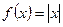 ,
, 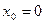 .
.
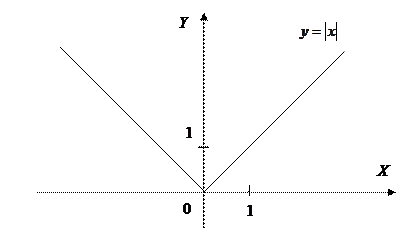
Функция 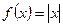 непрерывна в точке
непрерывна в точке 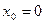 , так как
, так как 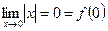 .
.
Найдём 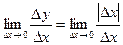 .
.
Рассмотрим односторонние пределы:
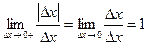 ;
; 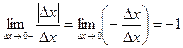 .
.
Отсюда 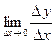 не существует, т.е. функция
не существует, т.е. функция 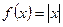 не имеет производной в точке
не имеет производной в точке 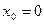 .
.
 2020-09-24
2020-09-24 110
110








