1. точки устранимого разрыва;
2. точки разрыва первого рода (скачки);
3. точки разрыва второго рода.
1. Примеры:
1) 
 - точка разрыва,
- точка разрыва,
 , функция не определена в точке
, функция не определена в точке  .
.

Продолжим функцию до непрерывности:

 функция
функция  непрерывна в точке
непрерывна в точке  .
.
2) 
 , тогда точка
, тогда точка  является точкой разрыва.
является точкой разрыва.

Переопределим значение функции в точке  , чтобы функция
, чтобы функция  стала непрерывной:
стала непрерывной:  .
.
Определение 2. Точка 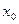 называется точкой устранимого разрыва функции
называется точкой устранимого разрыва функции  , если существует
, если существует  , но
, но  или значение функции
или значение функции  в точке
в точке  не задано.
не задано.
2. Определение 3. Точка 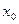 называется точкой разрыва первого рода функции
называется точкой разрыва первого рода функции  , если существуют конечные односторонние пределы
, если существуют конечные односторонние пределы  и
и  , но они различны, следовательно,
, но они различны, следовательно,  не существует.
не существует.
Пример:


 - точка разрыва,
- точка разрыва,
 ,
,
 ,
,
следовательно,  - точка разрыва первого рода.
- точка разрыва первого рода.
3. Определение 4. Точка 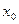 называется точкой разрыва второго рода функции
называется точкой разрыва второго рода функции  , если хотя бы один из односторонних пределов бесконечен или не существует.
, если хотя бы один из односторонних пределов бесконечен или не существует.
Примеры:
1) 

Рассмотрим точку  .
.
 ,
,  ,
,
следовательно,  - точка разрыва второго рода.
- точка разрыва второго рода.
2) 
 ,
, 
 ,
,  ,
,
 ,
,  ,
,
 ,
, 
 - точка разрыва второго рода.
- точка разрыва второго рода.
 , следовательно, прямая
, следовательно, прямая  является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции  .
.

3) 
 - не существует;
- не существует;
 - не существует.
- не существует.
 - точка разрыва второго рода.
- точка разрыва второго рода.
Свойства функций, непрерывных в точке.
Теорема 1. Сумма (разность) конечного числа функций, непрерывных в точке  , есть функция, непрерывная в точке
, есть функция, непрерывная в точке 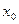 .
.
Теорема 2. Произведение конечного числа функций, непрерывных в точке 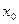 , есть функция, непрерывная в точке
, есть функция, непрерывная в точке 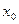 .
.
Теорема 3. Частное двух функций, непрерывных в точке 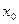 , есть функция, непрерывная в этой точке, если значение функции, стоящей в знаменателе, отлично от нуля в точке
, есть функция, непрерывная в этой точке, если значение функции, стоящей в знаменателе, отлично от нуля в точке 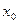 .
.
Пример:
Функция  непрерывна в любой точке
непрерывна в любой точке  как произведение двух непрерывных функций.
как произведение двух непрерывных функций.
РАЗДЕЛ 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Тема 6. ПРОИЗВОДНАЯ ФУНКЦИИ. ГЕОМЕТРИЧЕСКИЙ И МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
 2020-09-24
2020-09-24 149
149








