ВАРИАНТ 1
I часть (5 баллов)
При выполнении заданий 1 – 5 следуетзаписатьтолькоответ.
1. (1 балл) Точка А лежит вне плоскости α. Сколько можно провести через точку А прямых, параллельных плоскости α?
А) ни одной; Б) одну;
В) бесчисленное множество; Г) определить невозможно
2. (1 балл) Плоскость перпендикулярна одной из двух параллельных прямых. Как расположена вторая из этих прямых относительно данной плоскости?
А) параллельна плоскости; Б) перпендикулярна плоскости;
В) лежит в плоскости; Г) определить невозможно
3. (1 балл) Какое количество ребер может быть у призмы:
А) 2018; Б) 2019; В) 2020; Г) 2021?
4. (1 балл) Используя изображение куба 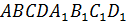 , найдите угол между прямыми
, найдите угол между прямыми 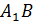 и
и 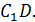
А) 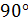 ; Б)
; Б) 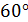 ; В)
; В) 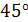 ; Г) прямые параллельны
; Г) прямые параллельны
5.
| M |
| A |
| B |
| C |
| K |
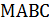 плоскости
плоскости 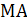 – высота. В треугольнике
– высота. В треугольнике 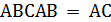 ;
; 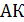 – медиана. Указать линейный угол двугранного угла при ребре ВС.
– медиана. Указать линейный угол двугранного угла при ребре ВС. А) 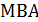 ; Б)
; Б) 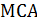 ; В)
; В) 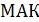 ; Г)
; Г) 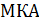
II часть (4 балла)
Решение заданий 6 – 7 должносодержатькраткуюзапись без обоснования. Правильноерешениекаждогозаданияоцениваетсядвумябаллами.
6. (2 балла) Точка 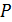 находится на расстоянии 9 см от каждой из вершин квадрата
находится на расстоянии 9 см от каждой из вершин квадрата 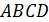 , сторона которого равна
, сторона которого равна 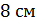 . Найдите расстояние от точки
. Найдите расстояние от точки 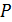 до плоскости квадрата.
до плоскости квадрата.
7. (2 балла) Даны две параллельные плоскости 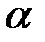 и
и 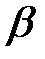 . Луч
. Луч 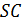 пересекает плоскость
пересекает плоскость 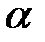 в точке
в точке 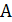 , а плоскость
, а плоскость 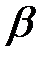 – в точке
– в точке 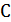 ; луч
; луч 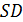 пересекает плоскость
пересекает плоскость 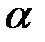 в точке
в точке 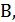 а плоскость
а плоскость 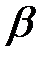 – в точке
– в точке 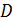 .
. 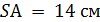 ,
, 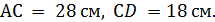 Найдите длину отрезка АВ.
Найдите длину отрезка АВ.
III часть (3 балла)
Решениезадания 8 должносодержатьобоснование. В нёмнеобходимозаписатьпоследовательныелогическиедействия и ихобъяснения
8. Сторона основания правильной треугольной призмы равна 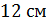 . Диагональ боковой грани образует с плоскостью основания угол
. Диагональ боковой грани образует с плоскостью основания угол 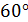 . Найдите площадь полной поверхности данной призмы.
. Найдите площадь полной поверхности данной призмы.
ВАРИАНТ 2
I часть (5 баллов)
При выполнении заданий 1 – 5 следуетзаписатьтолькоответ.
1. (1 балл) Даны две скрещивающиеся прямые 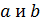 . Точки
. Точки 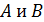 лежат на прямой
лежат на прямой 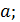 точки
точки 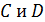 лежат на прямой
лежат на прямой 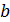 . Каково взаимное расположение прямых
. Каково взаимное расположение прямых 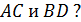
А) прямые параллельны; Б) скрещиваются;
В) пересекаются; Г) определить невозможно
 |
 |
 |
 |
 |
 |
 |
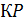 и его середину точку
и его середину точку 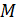 проведены параллельные прямые, пересекающие плоскость α в точках
проведены параллельные прямые, пересекающие плоскость α в точках 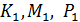 соответственно. Найти длину отрезка
соответственно. Найти длину отрезка 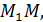 если
если 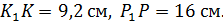
А) 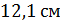 ; Б)
; Б) 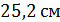 ;
;
В) 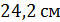 Г)
Г) 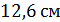
3. (1 балл) Из точки Р, удаленной от плоскости α на расстояние 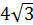 см, к этой плоскости проведена наклонная, образующая угол 60° с плоскостью α. Найти длину этой наклонной.
см, к этой плоскости проведена наклонная, образующая угол 60° с плоскостью α. Найти длину этой наклонной.
А) 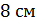 ; Б)
; Б) 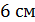 ; В)
; В) 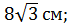 Г)
Г) 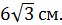
4. (1 балл) Найдите боковую поверхность прямой призмы, в основании которой лежит равнобедренный треугольник с боковой стороной 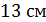 и основанием
и основанием 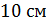 , если боковое ребро призмы равно
, если боковое ребро призмы равно 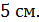
А) 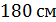 ; Б)
; Б) 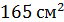 ; В)
; В) 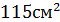 ; Г)
; Г) 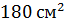
5. (1 балл) 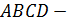 квадрат со стороной
квадрат со стороной 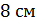 .
. 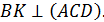 Найдите расстояние от точки
Найдите расстояние от точки 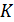 до прямой
до прямой 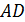 , если длина
, если длина 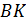 равна
равна 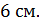
А) 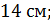 Б)
Б) 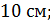 В)
В) 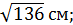 Г)
Г) 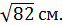
II часть (4 балла)
Решение заданий 6 – 7 должносодержатькраткуюзапись без обоснования. Правильноерешениекаждогозаданияоцениваетсядвумябаллами.
6. (2 балла) Сторона основания правильной шестиугольной пирамиды равна 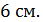 Боковые грани наклонены к основанию под углом
Боковые грани наклонены к основанию под углом 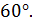 Найти площадь боковой поверхности пирамиды.
Найти площадь боковой поверхности пирамиды.
7. (2 балла) Чему равна полная поверхность прямого параллелепипеда с высотой, равной 5 см, в основании которого лежит параллелограмм со сторонами 6 см и 7 см и острым углом 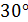 ?
?
III часть (3 балла)
Решениезадания 8 должносодержатьобоснование. В нёмнеобходимозаписатьпоследовательныелогическиедействия и ихобъяснения
8. Найдите высоту пирамиды 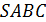 , если известно, что
, если известно, что 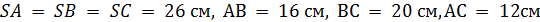 .
.
ВАРИАНТ 3
I часть (5 баллов)
При выполнении заданий 1 – 5 следуетзаписатьтолькоответ.
1. (1 балл) Даны две разные плоскости 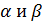 и точка
и точка 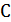 , не лежащая ни в одной из этих плоскостей. Сколько существует различных прямых, проходящих через точку
, не лежащая ни в одной из этих плоскостей. Сколько существует различных прямых, проходящих через точку 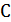 и не пересекающих ни одну из этих плоскостей?
и не пересекающих ни одну из этих плоскостей?
А) Ни одной; Б) одна;
В) бесчисленное множество; Г) определить невозможно
2. (1 балл) В треугольнике MKC KM⊥MC. Точка F не принадлежит плоскости треугольника и FM⊥MK. Какие утверждения верны?
1) FM⊥(MKC); 2) KM⊥(MFC);
3) KM⊥CF; 4) FM⊥CK.
А) 2) и 3); Б) 1) и 4); В) 3) Г) 1)
3. (1 балл) Измерения прямоугольного параллелепипеда равны 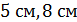 и
и 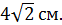 Чему равна диагональ параллелепипеда?
Чему равна диагональ параллелепипеда?
А) 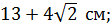 Б)
Б) 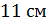 ;
;
В) 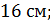 Г)
Г) 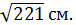
4.
| S |
| A |
| B |
| C |
| K |
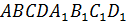 , найдите расстояние между
, найдите расстояние между 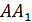 и
и 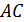 , если известно, что ребро куба равно
, если известно, что ребро куба равно 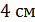 .
. А) 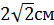 ; Б)
; Б) 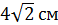 ;
;
В) 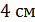 ; Г)
; Г) 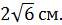
5. (1 балл) В пирамиде 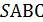 плоскости
плоскости 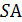 – высота. В треугольнике
– высота. В треугольнике 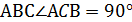 ;
; 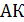 – биссектриса. Указать линейный угол двугранного угла при ребре ВС.
– биссектриса. Указать линейный угол двугранного угла при ребре ВС.
А) 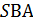 ; Б)
; Б) 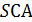 ; В)
; В) 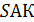 ; Г)
; Г) 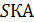
II часть (4 балла)
Решение заданий 6 – 7 должносодержатькраткуюзапись без обоснования. Правильноерешениекаждогозаданияоцениваетсядвумябаллами.
6. (2 балла) Сторона правильного треугольника 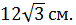 Точка
Точка 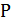 находится на расстоянии 10 см от сторон данного треугольника. Найти расстояние от точки Р до плоскости этого треугольника.
находится на расстоянии 10 см от сторон данного треугольника. Найти расстояние от точки Р до плоскости этого треугольника.
7. (2 балла) Параллельные прямые 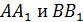 пересекают параллельные плоскости α и β в точках
пересекают параллельные плоскости α и β в точках 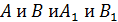 соответственно (
соответственно (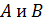 лежат на
лежат на 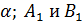 лежат на
лежат на 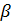 ). Найти периметр и площадь четырехугольника
). Найти периметр и площадь четырехугольника 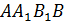 , если
, если 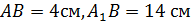 и
и 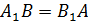 .
.
III часть (3 балла)
Решениезадания 8 должносодержатьобоснование. В нёмнеобходимозаписатьпоследовательныелогическиедействия и ихобъяснения
8. Высота правильной четырехугольной пирамиды равна 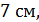 а боковое ребро равно
а боковое ребро равно 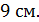 Найдите площадь полной поверхности данной пирамиды.
Найдите площадь полной поверхности данной пирамиды.
ВАРИАНТ 4
I часть (5 баллов)
При выполнении заданий 1 – 5 следуетзаписатьтолькоответ.
1. (1 балл) Какиеизнижеприведенныхутвержденийправильные:
1) Если прямая пересекает две диагонали трапеции, то она лежит в плоскости этой трапеции.
2) Если три вершины ромба принадлежат плоскости 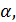 то все точки ромба лежат также в
то все точки ромба лежат также в 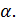
А) ни одно из утверждений; Б) только первое;
В) только второе; Г) оба утверждения верны
2. (1 балл) Какое количество ребер может быть у пирамиды:
А) 2017; Б) 2018; В) 2021; Г) 2023?
3. (1 балл) Найдите площадь диагонального сечения куба, ребро которого равно 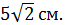
А) 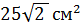 ; Б)
; Б) 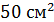 ;
;
В) 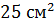 ; Г)
; Г) 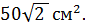
4. (1 балл) Найти полную поверхность правильной треугольной пирамиды, периметр основания которой равен 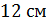 , а апофема
, а апофема 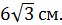
А) 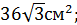 Б)
Б) 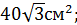 В)
В) 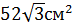 ; Г)
; Г) 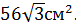
5. (1 балл) Плоскости 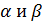 пересекаются по прямой
пересекаются по прямой 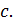 Точка
Точка 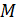 лежит в плоскости
лежит в плоскости 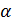 и удалена от прямой
и удалена от прямой 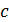 на расстояние, равное
на расстояние, равное 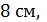 а от плоскости
а от плоскости 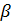 на расстояние, равное
на расстояние, равное 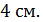 Найдите угол между данными плоскостями.
Найдите угол между данными плоскостями.
А) 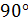 ; Б)
; Б) 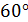 ; В)
; В) 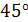 ; Г)
; Г) 
II часть (4 балла)
Решение заданий 6 – 7 должносодержатькраткуюзапись без обоснования. Правильноерешениекаждогозаданияоцениваетсядвумябаллами.
6. (2 балла) Из точки 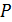 проведены к плоскости
проведены к плоскости 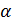 две наклонные
две наклонные 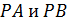 , каждая из которых наклонена к плоскости под углом
, каждая из которых наклонена к плоскости под углом 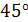 . Найти
. Найти 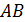 , если известно, что угол между наклонными равен
, если известно, что угол между наклонными равен 
7. (2 балла) Плоскости равностороннего треугольника 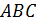 и квадрата
и квадрата 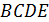 перпендикулярны. Найдите расстояние от точки
перпендикулярны. Найдите расстояние от точки 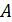 до прямой
до прямой 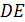 , если
, если 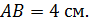
III часть (3 балла)
Решениезадания 8 должносодержатьобоснование. В нёмнеобходимозаписатьпоследовательныелогическиедействия и ихобъяснения
8. В основании прямой четырехугольной призмы лежит ромб с диагоналями 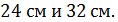 Найдите площадь полной поверхности этой призмы, если меньшая диагональ призмы равна
Найдите площадь полной поверхности этой призмы, если меньшая диагональ призмы равна 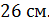
 2020-09-24
2020-09-24 1333
1333








