2020-09-24
246
Задача. Диагностика механизма осуществляется по температуре подшипниковых узлов. Установлено, что для исправного состояния среднее значение x 0подшипникового узла составляет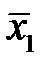 
=50°C и среднее квадратичное отклонение σ 1=15°C. При наличии повышенного износа, где 
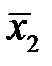=100°C, σ 2=25°C, распределения предполагаются нормальными.
В результате измерений получены данные, приведённые в табл. 2.1. Выбирая из массива последовательно точки измерений, необходимо определить номер измерения, после которого будет превышен порог.
Содержание отчёта
1. Название расчёта, задача и номер варианта;
2. Расчётные формулы с пояснительным текстом;
3. Расчётные формулы с численными значениями;
4. Выводы по работе.
Таблица 2.1
Исходные данные для задачи
| № вар. | α; β | 1 | 2 | 3 | 4 | 5 | 6 |
| 1. | 0,1;0,1 | 71 | 52 | 83 | 132 | 46 | 78 |
| 2. | 0,1; 0,05 | 107 | 48 | 75 | 97 | 67 | 89 |
| 3. | 0,05; 0,1 | 78 | 52 | 72 | 98 | 70 | 36 |
| 4. | 0,05;0,05 | 88 | 114 | 97 | 90 | 128 | 27 |
| 5. | 0,01;0,05 | 79 | 110 | 83 | 96 | 36 | 68 |
| 6. | 0,05;0,01 | 47 | 37 | 62 | 66 | 92 | 93 |
| 7. | 0,1;0,1 | 88 | 72 | 71 | 86 | 62 | 87 |
| 8. | 0,1; 0,05 | 70 | 60 | 103 | 104 | 27 | 115 |
| 9. | 0,05; 0,1 | 102 | 66 | 116 | 103 | 80 | 19 |
| 10. | 0,05;0,05 | 74 | 94 | 69 | 85 | 41 | 28 |
| 11. | 0,01;0,05 | 77 | 96 | 86 | 60 | 103 | 78 |
| 12. | 0,05;0,01 | 75 | 94 | 94 | 84 | 97 | 84 |
| 13. | 0,1;0,1 | 55 | 88 | 87 | 95 | 81 | 77 |
| 14. | 0,1; 0,05 | 90 | 80 | 86 | 87 | 91 | 68 |
| 15. | 0,05; 0,1 | 113 | 89 | 49 | 103 | 82 | 109 |
| 16. | 0,05;0,05 | 99 | 111 | 72 | 68 | 111 | 75 |
| 17. | 0,01;0,05 | 85 | 81 | 69 | 66 | 88 | 103 |
| 18. | 0,05;0,01 | 92 | 47 | 116 | 77 | 113 | 84 |
| 19. | 0,1;0,1 | 93 | 80 | 63 | 72 | 83 | 78 |
| 20. | 0,1; 0,05 | 93 | 80 | 60 | 102 | 103 | 104 |
| 21. | 0,05; 0,1 | 54 | 45 | 50 | 63 | 45 | 79 |
| 22. | 0,05;0,05 | 64 | 52 | 76 | 45 | 92 | 72 |
| 23. | 0,01;0,05 | 57 | 50 | 80 | 64 | 78 | 83 |
| 24. | 0,05;0,01 | 66 | 77 | 66 | 29 | 85 | 60 |
| 25. | 0,1;0,1 | 73 | 57 | 80 | 67 | 50 | 56 |
| 26. | 0,1; 0,05 | 54 | 69 | 63 | 61 | 72 | 67 |
| 27. | 0,05; 0,1 | 75 | 52 | 20 | 45 | 86 | 67 |
| 28. | 0,05;0,05 | 69 | 51 | 45 | 69 | 44 | 77 |
| 29. | 0,01;0,05 | 63 | 43 | 27 | 57 | 49 | 95 |
| 30. | 0,05;0,01 | 52 | 53 | 59 | 61 | 63 | 67 |
| 31. | 0,1;0,1 | 75 | 94 | 94 | 84 | 97 | 84 |
| 32. | 0,1; 0,05 | 55 | 88 | 87 | 95 | 81 | 77 |
| 33. | 0,05; 0,1 | 90 | 80 | 86 | 87 | 91 | 68 |
| 34. | 0,05;0,05 | 113 | 89 | 49 | 103 | 82 | 109 |
| 35. | 0,01;0,05 | 99 | 111 | 72 | 68 | 111 | 75 |
| 36. | 0,05;0,01 | 85 | 81 | 69 | 66 | 88 | 103 |
|
|
|
3 Объем испытаний методом
последовательного анализа
Средний объем испытаний методом последовательного анализа для различных законов распределения наработки на отказ при справедливости гипотезы H 0 выражается соотношением [6, 10, 13, 14, 15]
 ;
| (3.1) |
где 
– математическое ожидание случайной величины из последовательности наблюдений, при которых параметр θ принимает значение θ 0.
Соответственно при справедливости гипотезы H 1 средний объем испытаний равен:
 .
| (3.2) |
В [6, с. 127, 13, с. 377] приведены формулы для определения границ приёмки и отбраковки:
 ;
| (3.3) |
 .
| (3.4) |
При каждом m – число текущих испытаний, правая часть неравенства (3.4) обозначена через mПР и называется приёмочным числом или границей приёмки. Аналогично правая часть (3.3) обозначена mБР и называется браковочным числом или границей браковки [14, с. 201]
|
|
|
