Обратимые матрицы. Элементарные матрицы. Леммы 1-2

Матрицы. Нулевая матрица. Единичная матрица. Операции над матрицами

Поле – некоторое множество с введёнными над этим множеством операциями сложения, вычитания, умножения, деления и выделенным нейтральным элементом, относительно операции умножения.

 – матрица или матрица над полем L  – это таблица вида 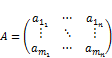, при чём 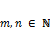, а 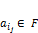, где F – множество скаляров, по которым введены основные арифметические операции в поле  с нейтральным элементом 1.

Для её обозначения используют символ: 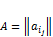, где , , 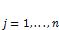где i – номер строки, а j – номер столбца, а множество всех  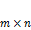- матриц обозначают через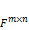

· Если , то матрица – прямоугольная.

· Если 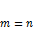, то матрица – квадратная.

Все элементы  матрицы 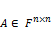 при i = j называются элементами главной диагонали

· Матрица называется нулевой, если все её элементы равны 0 (обозначается через латинскую букву ).

· Матрица называется единичной, если элементы её главной диагонали равны 1, а вне этой диагонали равны 0 (обозначается через латинскую букву ).

 

Матрицы равны, если совпадают их размерности и соответствующие элементы.

Чтобы сложить матрицы одинаковых размерностей следует сложить их соответствующие элементы, аналогично с вычитанием.

Умножение на скаляр: 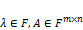, тогда , где ,

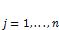
Матрица 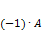  противоположна матрице . При этом выполняется условие .

Умножение матриц: при умножении матриц  важно учитывать, что количество столбцов в A должно совпадать c количеством строк в B. Если 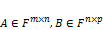, то результатом будем матрица размерностью .  Для большего понимания можно элементы из этого изображения, где элемент первой строки второго столбца, например, считается как :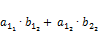

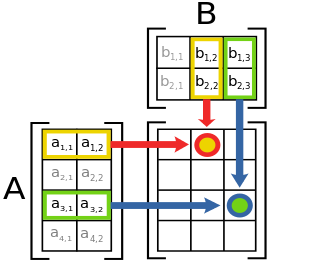
Свойства операций над матрицами.

Для любых двух матриц  справедливо:

1.

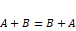
2.

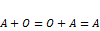
3. , где  – скаляр

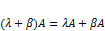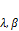4. , где  – скаляры

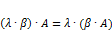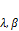5. , где  – скаляры

6. 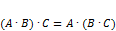, где C – матрица и ,

7. 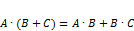, если ,  и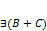

8.

Транспонированные матрицы. Теорема о транспонировании произведения квадратных матриц

Транспонированная матрица получается заменой в матрице строк соответствующими столбцами (обозначается через ).

Теорема. Если 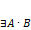 и , то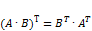

Обратимые матрицы. Элементарные матрицы. Леммы 1-2

Обратимыми называют квадратные матрицы, произведение которых даёт единичную матрицу (обозначается через ).

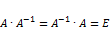, где 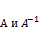 называются  взаимообратными по отношению друг к другу.

Теорема. Если матрица A обратима, то существует только одна матрица обратная к ней.

Следствие. Произведение любого числа обратимых матриц есть также обратимая матрица.

Элементарная матрица – квадратная матрица, получающаяся из единичной матрицы в результате неособенных элементарных преобразований.

К неособенным элементарным преобразованиям относят:

1. умножение элементов какой-либо строки/столбца на отличное от 0 число

2. прибавление к элементам какой-либо строки/столбца элементов другой строки/столбца, умноженных на

Лемма 1. Всякая элементарная матрица является обратимой, при чём матрица, обратная, элементарной, снова является элементарной матрицей.

Лемма 2. Произведение элементарных матриц есть обратимая матрица.