Условие обратимости квадратных матриц. Леммы 1-3. Вычисления обратной матрицы. Теорема

Векторы 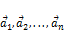  линейно-зависимы, если существуют  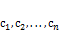одновременно неравные 0 и такие, что выполняется равенство: .

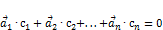Векторы 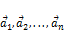  линейно-независимы, если равенство  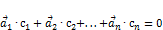выполняется только при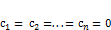

Лемма 1. Квадратная матрица, содержащая 0-ую строку, является необратимой.

Лемма 2. Если в квадратной матрице строки линейно-зависимы, то матрица необратима, вследствие второй леммы.

Лемма 3. Если строки квадратной матрицы линейно-независимы, то матрицу можно представить в виде …

Замечание (следуетиз лемм 2, 3). Если в квадратной матрице строки линейно-независимы, то матрица – обратима.

Теорема. Если за конечное число применение неособенных элементарных преобразований получается единичная матрица, то квадратная матрица является обратимой, при чём эта же цепочка неособенных элементарных преобразований приводит матрицу той же самой размерности, что и исходная квадратная матрица, в матрицу, обратную ей.

Найдём матрицу, обратную матрице  :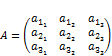

1. Составим расширенную матрицу.

2. Обнулим элементы ниже главной диагонали при помощи неособенных элементарных преобразований.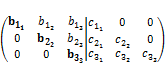

3. Аналогично обнулим элементы выше главной диагонали.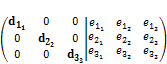

4. Умножаем каждую строку на элемент этой строки в главной диагонали, возведённый в минус первую степень (делим на элемент этой строки в главной диагонали).

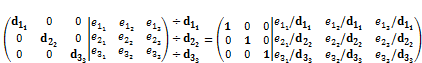
5. Получившаяся справа от черты матрица 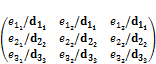 и есть матрица, обратная матрице A (или матрица A^-1).

6. Проверить себя можно умножив матрицу A на получившуюся матрицу A^-1, при этом должна получиться единичная матрица.