Определение предела функции в точке. Односторонние пределы функции одной переменной. Бесконечно малые и бесконечно большие функции, их сравнение. Свойства сходящихся в точке функций: ограниченность функции в окрестности точки схождения, действия над сходящимися функциями. Эквивалентные функции, их использование при определении предела отношения функций. Первый и второй замечательные пределы. Таблица важнейших пределов. Определение пределов степенно-показательных функций. Непрерывность функции. Определение и классификация точек разрыва. Кусочно-непрерывные функции.
Литература:
Высшая математика. Практикум, Ч. 1 / А. В. Конюх, С. В. Майоровская, О. Н. Поддубная, В. А. Рабцевич. – Минск: [б. и.], 2014. – 274 с.
Задачи для самостоятельного решения:
5.3.1. Найти предел функции
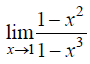
5.3.2. Найти предел функции
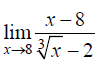
5.3.3. Найти предел функции
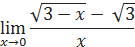
Задания, которые необходимо сдать на аттестацию
Межсессионная аттестация
Задачи для самостоятельного решения (оформляются как контрольная работа):
1.2.1. Запишите формулу для афоризма Конфуция «Благородный человек предъявляет требования к себе, низкий человек предъявляет требования к другим».
1.2.2. Составьте таблицу истинности для формулы A ˅ B → 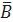 ˅ C.
˅ C.
1.2.3. Установить равносильность суждений: «Если взялся за дело, то доведи его до конца» и «Не берись за дело или доведи его до конца».
1.3.1. Найдите сумму и разность комплексных чисел 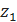 = 2 – i,
= 2 – i, 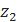 = –3 + 4i.
= –3 + 4i.
1.3.2. Найдите произведение и частное комплексных чисел 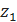 = 4+4i,
= 4+4i, 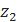 = – 2 – i.
= – 2 – i.
1.3.3. Запишите заданное комплексное число в тригонометрической и показательной формах z = 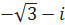 .
.
1.3.4. Найдите 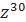 , если z = −
, если z = − 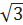 + i.
+ i.
1.3.5. Решите уравнение на множестве комплексных чисел 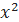 – 4 = 0.
– 4 = 0.
2.1.1. Найти матрицу C = A – 3B, если A =  , B =
, B =  .
.
2.1.2. Вычислить А·В и В·А, если A = 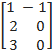 , В =
, В = 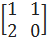 .
.
2.1.3. Найти транспонированную матрицу для A = 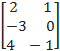 . Вычислить А·
. Вычислить А· 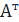 и
и 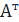 ·А.
·А.
2.1.4. Вычислить определитель 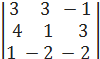 .
.
2.2.1. Решить систему линейных алгебраических уравнений методом Гаусса, Крамера и матричным методом
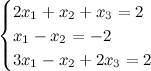
 2020-09-24
2020-09-24 109
109








