Конспект лекций по дисциплине «Математический анализ»
Тема №1
Действительные числа и их свойства
Лекция №1
1. Множества.
2. Множество действительных чисел.
3. Аксиомы множества действительных чисел.
4. Сравнение действительных чисел или упорядоченность.
5. Принцип Дедекинда.
6. Дополнительные свойства действительных чисел.
Множества
В математике первичными понятиями являются понятия множества, элемента множества и принадлежности элемента множеству.
Теория множеств будет Вам подробно прочитана в дисциплине «Алгебра и теория чисел». В дисциплине математического анализа мы лишь фрагментарно коснемся общих понятий теории множеств. Это нам нужно для того, чтобы перейти к вопросу «Множество действительных чисел».
Определение №1. Множеством называется совокупность объектов, которые мы объединяем в одну группу (по произвольному признаку). Причем, с точки зрения теории множеств природа этих объектов несущественна.
Определение №2. Объекты, из которых состоит множество, называются его элементами.
Примеры множеств: а) множество студентов в данной аудитории М 28;
б) множество натуральных чисел  , т. е. все положительные целые числа
, т. е. все положительные целые числа 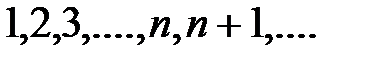 ;
;
в) семейство звезд созвездия Большой Медведицы – тоже множество.
Обозначения. Логические символы
Как правило, множества обозначают большими, а их элементы малыми буквами латинского алфавита.
1) Если 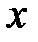 – элемент множества
– элемент множества 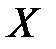 , то пишут
, то пишут 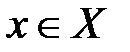 (
(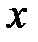 принадлежит
принадлежит 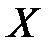 ).
).
Пример. Число 7 принадлежит множеству натуральных чисел  .
.
2) Если 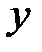 не является элементом множества
не является элементом множества 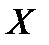 , то пишут
, то пишут 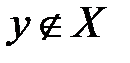 или
или 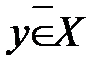 (
(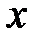 не принадлежит множеству
не принадлежит множеству 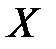 ).
).
Пример. Так число 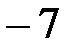 не принадлежит множеству натуральных чисел,
не принадлежит множеству натуральных чисел, 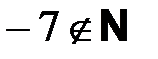 .
.
3) Если 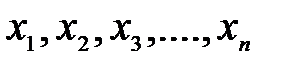 – некоторые элементы, то запись
– некоторые элементы, то запись 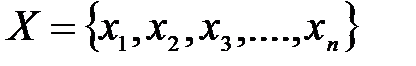 означает, что множество
означает, что множество 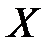 состоит из элементов
состоит из элементов 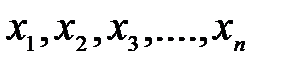 .
.
Пример. Аналогичный смысл имеет запись 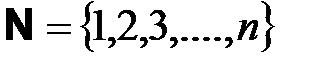 .
.
4) Пусть 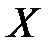 и
и 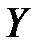 – два множества. Если
– два множества. Если 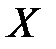 и
и 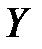 состоят из одних и тех же элементов, то говорят, что множества
состоят из одних и тех же элементов, то говорят, что множества 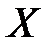 и
и 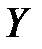 совпадают. А пишут
совпадают. А пишут 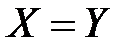 .
.
Пример. 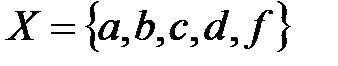 ;
; 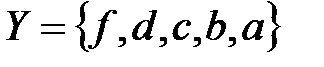 , то
, то 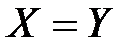 , так как порядок расположения элементов во множестве не имеет значения.
, так как порядок расположения элементов во множестве не имеет значения.
5) Если во множестве 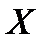 нет элементов, не принадлежащих множеству
нет элементов, не принадлежащих множеству 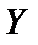 , то говорят, что множество
, то говорят, что множество 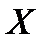 содержится во множестве
содержится во множестве 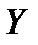 и пишут
и пишут
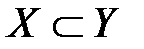 (
(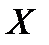 содержится в
содержится в 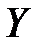 ) или
) или 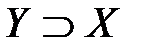 (
(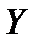 содержит
содержит 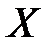 ).
).
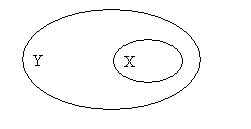
Тогда множество 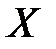 называют подмножеством множества
называют подмножеством множества 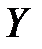 .
.
Пример. Множество натуральных чисел является подмножеством множества целых чисел, т.е. 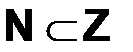 .
.
6) Если множество 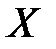 не содержится во множестве
не содержится во множестве 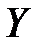 , то пишут
, то пишут 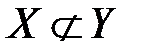 .
.
Пример. Пусть множество 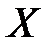 – множество отрицательных чисел, то
– множество отрицательных чисел, то 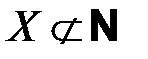 . Оно не содержится во множестве натуральных чисел.
. Оно не содержится во множестве натуральных чисел.
7) В математике часто используется пустое множество. Оно не содержит ни одного элемента и обозначается  .
.
Очевидно, что пустое множество является подмножеством любого множества.
Пример.  , пустое множество является подмножеством множества натуральных чисел.
, пустое множество является подмножеством множества натуральных чисел.
8) Если множество 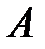 состоит из элементов, обладающих определенным свойством, то пишут
состоит из элементов, обладающих определенным свойством, то пишут 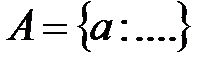 или
или 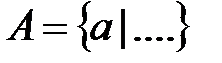 . Здесь в фигурных скобках после двоеточия или вертикальной черты записывается указанное свойство элементов множества
. Здесь в фигурных скобках после двоеточия или вертикальной черты записывается указанное свойство элементов множества 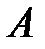 .
.
Пример. Пусть 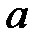 и
и 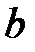 – два действительных числа, причем
– два действительных числа, причем 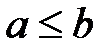 . И пусть через отрезок
. И пусть через отрезок 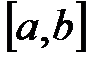 обозначено множество всех действительных чисел
обозначено множество всех действительных чисел 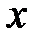 , удовлетворяющих неравенству
, удовлетворяющих неравенству 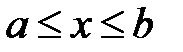 . Тогда определение этого множества, обозначенного отрезком
. Тогда определение этого множества, обозначенного отрезком 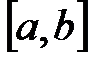 , посредством указанных символов можно записать следующим образом:
, посредством указанных символов можно записать следующим образом: 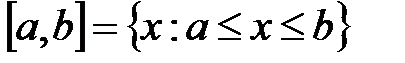 .
.
9) Пусть заданы два множества 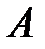 и
и 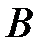 :
:
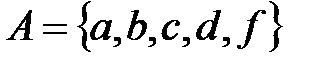 ;
; 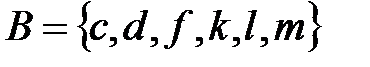
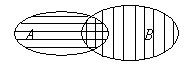
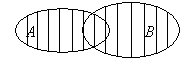
а) Тогда с помощью символа 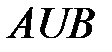 обозначается множество, называемое объединением (или суммой) множеств
обозначается множество, называемое объединением (или суммой) множеств 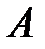 и
и 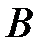 . Каждый элемент этого множества принадлежит хотя бы одному из множеств
. Каждый элемент этого множества принадлежит хотя бы одному из множеств 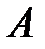 и
и 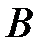 , либо им обоим. Графически объединение множеств
, либо им обоим. Графически объединение множеств 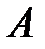 и
и 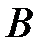 представлено на рисунке:
представлено на рисунке:
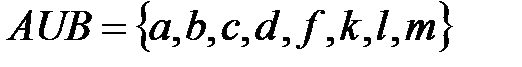
б) С помощью символа 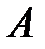
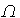
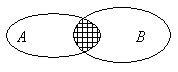
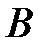 обозначается множество, называемое пересечением множеств
обозначается множество, называемое пересечением множеств 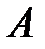 и
и 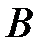 . Множество
. Множество 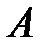
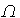
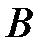 состоит из элементов, принадлежащих одновременно множеству
состоит из элементов, принадлежащих одновременно множеству 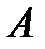 и множеству
и множеству 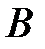 . Графически пересечение множеств
. Графически пересечение множеств 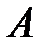
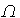
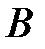 представлено на рисунке:
представлено на рисунке:

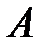
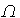
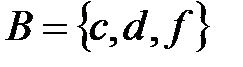
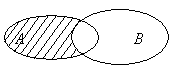
в) С помощью символа 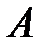 \
\ 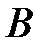 обозначается множество, называемое разностью множеств
обозначается множество, называемое разностью множеств 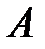 и
и 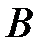 . Данное множество состоит из элементов, которые принадлежат множеству
. Данное множество состоит из элементов, которые принадлежат множеству 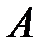 , но не принадлежат множеству
, но не принадлежат множеству 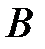 . Графически разность множеств
. Графически разность множеств 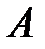 и
и 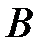 показано на рисунке:
показано на рисунке:
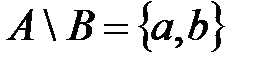
г) Если множество 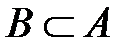 (содержится во множестве
(содержится во множестве 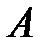 ), то разность множеств
), то разность множеств 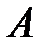 \
\ 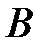 называется дополнением множества
называется дополнением множества 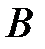 до множества
до множества 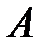 . Графически это выглядит так:
. Графически это выглядит так:
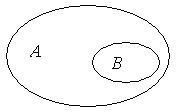
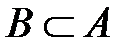 , то
, то 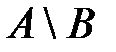
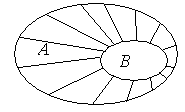
Разность 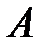 \
\ 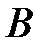 показана штриховкой. В этом случае говорят, что разность множеств
показана штриховкой. В этом случае говорят, что разность множеств 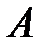 \
\ 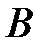 получается вычитанием из множества
получается вычитанием из множества 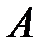 множества
множества 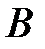 .
.
Пример. Пусть 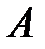 – множество студентов I курса факультета математики и информатики.
– множество студентов I курса факультета математики и информатики. 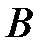 – множество девушек I курса факультета математики и информатики. Тогда разность
– множество девушек I курса факультета математики и информатики. Тогда разность 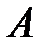 \
\ 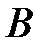 – есть множество юношей I курса факультета математики и информатики.
– есть множество юношей I курса факультета математики и информатики.
10) Если 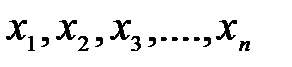 – произвольные числа, то запись
– произвольные числа, то запись 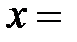 max
max 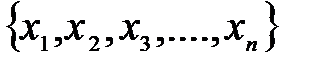 (или
(или 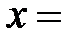 min
min 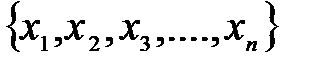 ) означает, что число
) означает, что число 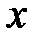 – максимальное (минимальное) из чисел
– максимальное (минимальное) из чисел 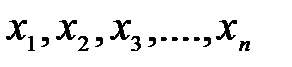 .
.
 2020-10-10
2020-10-10 242
242







