2020-10-10
179
В элементарной математике изучаются действительные числа. Их иногда называют еще вещественными.
Сначала в процессе счета возникает так называемый натуральный ряд чисел или множество натуральных чисел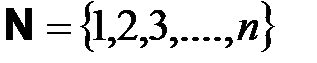 
. В арифметике вводятся действия сложения и умножения над натуральными числами. Операции деления и вычитания не всегда оказываются возможными во множестве натуральных чисел (
?; 
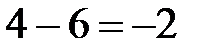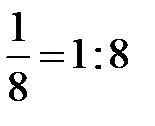?; и т. д.).
Для того чтобы все четыре арифметические операции были возможны, кроме операции деления на ноль, приходится расширить запас чисел. Причем, этого расширения запаса чисел требуют и измерения тех или иных физических и геометрических величин.
Поэтому вводятся число ноль и целые отрицательные числа вида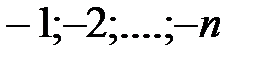 
– множество целых чисел, 
.
А затем вводятся и рациональные числа вида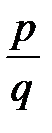 
, где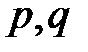 
– целые числа при 
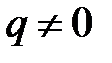– множество рациональных чисел, 
.
Та же потребность измерения величин и проведение таких операций, как извлечение корня, вычисление логарифмов, решение алгебраических уравнений приводит к дальнейшему расширению запаса рассматриваемых чисел.
Так появляются иррациональные числа, 
и, наконец, комплексные числа, 
.
Вспомним из школьного курса математики:
1) Целые числа – натуральные числа (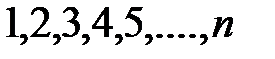
), числа им противоположные (
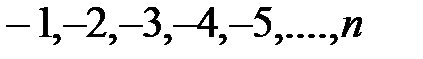) и число 0, (
).
2) Рациональные числа – целые числа, отрицательные, положительные и дробные числа, (
).
Причем: всякое рациональное число является либо целым, либо представляется конечной или бесконечной периодической десятичной дробью.
Пример. Конечная: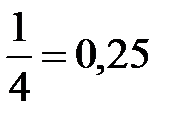 
; бесконечная периодическая десятичная дробь: 
.
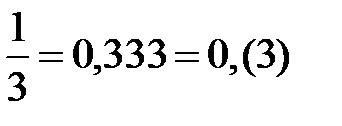3) Иррациональные числа – числа, которые представляются непериодической бесконечной десятичной дробью, например, число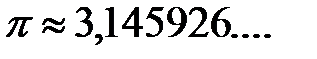 
; 
.
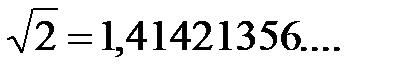4) Все рациональные и все иррациональные числа образуют множество всех действительных чисел,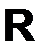 
(от латинского слова «действительный» или английского слова Real – реальный).
А теперь систематизируем сведения о действительных числах, перечислим основные свойства действительных чисел, а затем выведем из них некоторые следствия.
