Определение №1. Функции, принимающие числовые значения называются числовыми функциями.
Над числовыми функциями можно выполнять различные арифметические операции: если даны две числовые функции 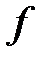 и
и 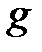 , определенные на одном и том же числовом множестве
, определенные на одном и том же числовом множестве  , то
, то
1) Функция 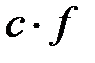 определяется как функция, принимающая в каждой точке
определяется как функция, принимающая в каждой точке  значение
значение  , где
, где 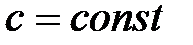 .
.
2) Функция 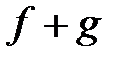 определяется как функция, принимающая в каждой точке
определяется как функция, принимающая в каждой точке 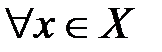 значение
значение  .
.
3) Функция 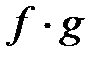 определяется как функция, принимающая в каждой точке значение
определяется как функция, принимающая в каждой точке значение  .
.
4) Функция 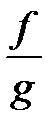 определяется как функция, принимающая в каждой точке значение
определяется как функция, принимающая в каждой точке значение 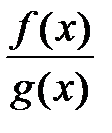 при
при 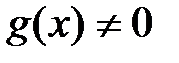 .
.
Определение №2. Функция, все значения которой равны между собой называется постоянной и обозначают  .
.
Ограниченные сверху, снизу и ограниченные функции
Определение №1. Функция  , определенная на некотором множестве
, определенная на некотором множестве  , называется ограниченной сверху на этом множестве, если существует такое число
, называется ограниченной сверху на этом множестве, если существует такое число 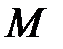 , что для любого
, что для любого 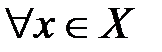 выполняется неравенство:
выполняется неравенство:  .
.
Определение №2. Функция  , определенная на некотором множестве
, определенная на некотором множестве  , называется ограниченной снизу на этом множестве, если существует такое число
, называется ограниченной снизу на этом множестве, если существует такое число 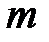 , что для любого
, что для любого 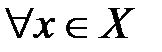 выполняется неравенство
выполняется неравенство  .
.
Определение №3. Функция 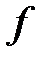 , ограниченная сверху и снизу на множестве
, ограниченная сверху и снизу на множестве  , называется ограниченной на этом множестве.
, называется ограниченной на этом множестве.
Очевидно, что функция 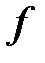 ограничена на множестве
ограничена на множестве  тогда, когда существует такое число
тогда, когда существует такое число  , что для любого
, что для любого 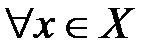 выполняется неравенство
выполняется неравенство 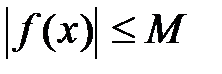 или
или 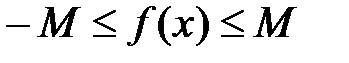 .
.
Верхняя и нижняя грани функции
Определение №1. Верхняя грань множества значений 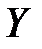 числовой функции
числовой функции  , определенной на множестве
, определенной на множестве  , называется верхней гранью функции
, называется верхней гранью функции 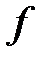 . Обозначение:
. Обозначение: 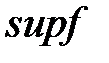 или
или 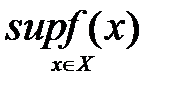 .
.
Определение №2. Нижняя грань множества значений 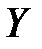 числовой функции
числовой функции 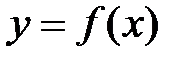 , определенной на множестве
, определенной на множестве  , называется нижней гранью функции
, называется нижней гранью функции 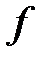 . Обозначение:
. Обозначение: 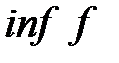 или
или 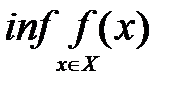 .
.
Замечание. 1. Верхняя (нижняя) грань функции может быть как конечной, так и бесконечной.
2. Функция ограничена сверху (снизу) на множестве  тогда и только тогда, когда она имеет на этом множестве конечную верхнюю (нижнюю) грань.
тогда и только тогда, когда она имеет на этом множестве конечную верхнюю (нижнюю) грань.
 2020-10-10
2020-10-10 231
231








