Определение №1. Функция  , определенная на множестве
, определенная на множестве  , принимает в точке
, принимает в точке 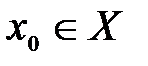 наибольшие (наименьшие) значения, если
наибольшие (наименьшие) значения, если 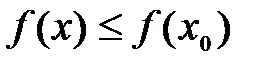

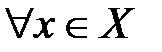 .
.
Определение №2. Наибольшие (наименьшие) значения функции называется также максимальным (минимальным) значением и пишется: 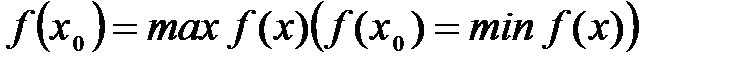 или
или 
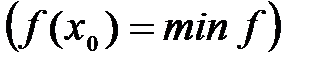 .
.
Определение №3. 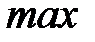 и
и  значения функции называются экстремальными.
значения функции называются экстремальными.
График функции
Определение №1. График функции – это множество пар точек  , координаты которых связаны соотношением
, координаты которых связаны соотношением 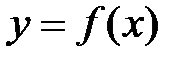 .
.
Определение №2. Соотношение  называется уравнением графика функции.
называется уравнением графика функции.
Пример: График функции 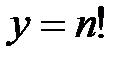 состоит из отдельных точек (рис.1.).
состоит из отдельных точек (рис.1.).
8  4 4
|
Рис.1. Рис.2.
Замечание. Не всякая линия является графиком какой-либо одной функции.
Пример. Уравнение окружности  не является графиком одной функции, так как каждое
не является графиком одной функции, так как каждое  входит не в одну, а в две пары чисел
входит не в одну, а в две пары чисел 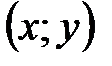 этого множества
этого множества  .
.  и
и  , где
, где 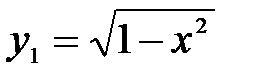 ;
; 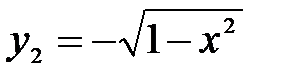 .
.
А это противоречит требованию однозначности в определении функций. Но часть окружности, лежащая в нижней полуплоскости, является графиком функции  . А другая часть окружности, лежащая в верхней полуплоскости, является графиком функции
. А другая часть окружности, лежащая в верхней полуплоскости, является графиком функции 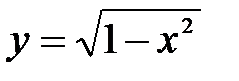 .
.
Способы задания функции
Определение. Задать функцию 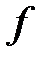 – это значит, указать, как по каждому значению аргумента
– это значит, указать, как по каждому значению аргумента 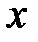 найти соответствующие ему значения функции
найти соответствующие ему значения функции  .
.
Существует три способа задания функции: аналитический, табличный и графический.
I. Аналитический явный способ задания функции
Сущность способа: Зависимость между переменными величинами определяется с помощью формулы. Она указывает, какие действия надо выполнить, чтобы получить значение функции, соответствующие данному значению аргумента.
Пример: Формула  (сигнум с латинского языка «знак») задает функцию
(сигнум с латинского языка «знак») задает функцию 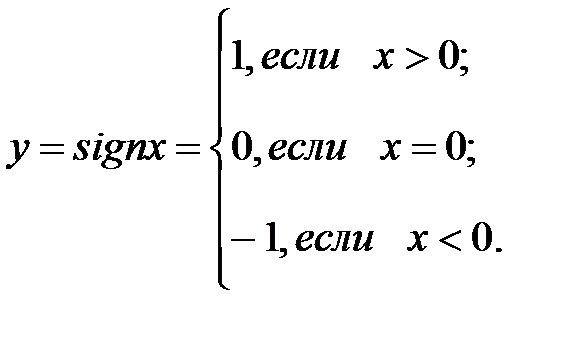
Рис.3.
Данная функция задана с помощью нескольких формул. Эта функция определена на всей числовой прямой. А множество ее значений состоит из –1;0;1.
2. Функция Дирихле 
определена на всей числовой прямой. А множество ее значений состоит из двух чисел: 1,0. Функцию Дирихле графически изобразить нельзя.
 , определенная на множестве
, определенная на множестве  , принимает в точке
, принимает в точке 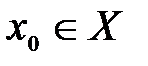 наибольшие (наименьшие) значения, если
наибольшие (наименьшие) значения, если 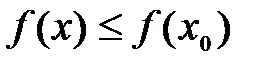

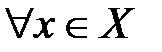 .
.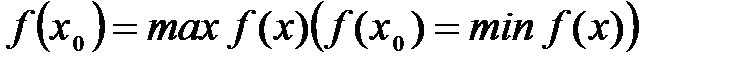 или
или 
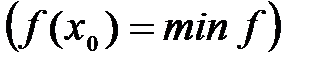 .
.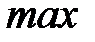 и
и  значения функции называются экстремальными.
значения функции называются экстремальными. , координаты которых связаны соотношением
, координаты которых связаны соотношением 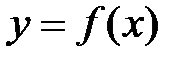 .
. называется уравнением графика функции.
называется уравнением графика функции.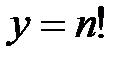 состоит из отдельных точек (рис.1.).
состоит из отдельных точек (рис.1.). 4
 не является графиком одной функции, так как каждое
не является графиком одной функции, так как каждое  входит не в одну, а в две пары чисел
входит не в одну, а в две пары чисел 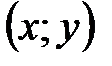 этого множества
этого множества  .
.  и
и  , где
, где 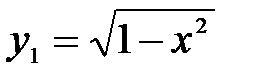 ;
; 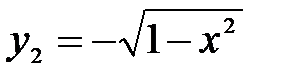 .
. . А другая часть окружности, лежащая в верхней полуплоскости, является графиком функции
. А другая часть окружности, лежащая в верхней полуплоскости, является графиком функции 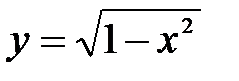 .
.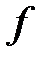 – это значит, указать, как по каждому значению аргумента
– это значит, указать, как по каждому значению аргумента 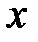 найти соответствующие ему значения функции
найти соответствующие ему значения функции  .
.  (сигнум с латинского языка «знак») задает функцию
(сигнум с латинского языка «знак») задает функцию 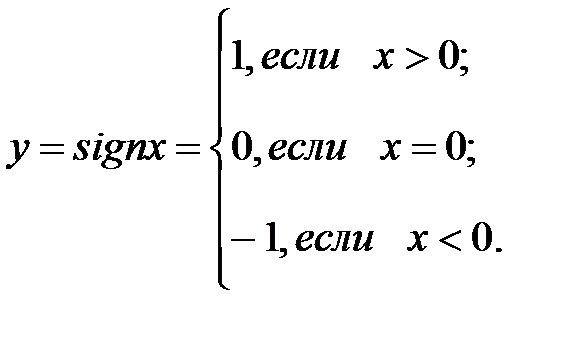

 2020-10-10
2020-10-10 158
158








