II. Аналитически неявный способ задания функции

1. Неявные функции

Определение. Пусть задано уравнение вида , т.е. задана функция двух действительных переменных и . Причем, рассматриваются только такие пары (если они существуют), для которых выполняется условие . Функции, задаваемые таким образом, называются неявными.

Замечание. 1. Термин «неявная» отражает не характер функциональной зависимости, а лишь способ ее задания.

2. Одна и та же функция может быть задана как явно, так и неявно.

Пример: Функции, заданные явно могут быть заданы и неявным образом с помощью уравнения: .

3. Сложные функции

Если заданы функции и , причем, область определения функции содержит множество значений функции 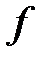, тогда каждому из области определения функции 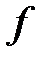естественным образом соответствует такое, что , где .

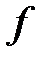Определение. Функция, определяемая соотношением называется сложной функцией или, композицией функций или суперпозицией функций и и обозначается т.е.

Сложная функция отражает не характер функциональной зависимости, а лишь способ ее задания.

Пример. . Данную функцию можно рассматривать как суперпозицию следующих функций: ; ; ; ; .

III. Табличный способ задания функции

Пусть дана таблица

x	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7
y	−1	0	1	2	3	4	5	6

Поставим в соответствие каждому значению 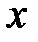, записанному в первой строке таблицы, число 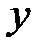, стоящее во второй строке под числом 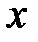. Тогда, можно сказать, что функция задана таблично. Областью определения этой функции является множество, состоящее из 8 чисел 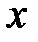. Они перечислены в первой строке таблицы. Множеством значений этой функции является множества, состоящее из 8 чисел , перечисленных во второй строке. С помощью таблицы можно задать функцию только при конечном числе значений аргумента. Таблицы часто используются для задания функции.