Практика 2 (неделя с 7 по 13 сентября)

Томский государственный университет систем управления и радиоэлектроники

Приходовский М.А.

Математика - 3 семестр

Курс практических занятий

Учебное пособие

Группы 519-1-2, 529, 539.

Томск

ТУСУР

2020

Оглавление по темам

 

Оглавление по номерам практик

Практика № 1...................................................... 3

Практика № 2........................................................11

Практика № 3........................................................20

Практика № 4........................................................28

Практика № 5........................................................35

Практика № 6........................................................

Практика № 7........................................................

Практика № 8........................................................

Практика № 9........................................................

 

Практика 1 (неделя до 6 сентября).

Комплексные числа

Задача 1. Умножить и поделить в алгебраической форме числа 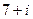 и .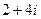

Решение.  Умножим эти числа.  =  =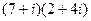

 = .

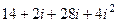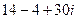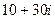Поделим, с помощью умножения на сопряжённое:

 =  =  =  =  =  = .

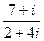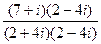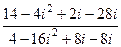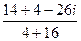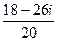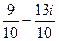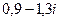Ответ. 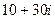 и .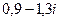

Задача 2.    Умножить и поделить .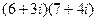

Решение.  =  =  = .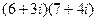

 =  =  =  = .

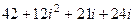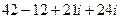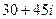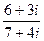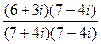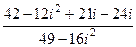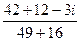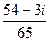Ответ. 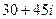 и .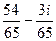 

Задача 3. Разделить 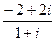 тремя способами:

1) с помощью умножения на сопряжённое число

2) в тригонометрической форме.

3) в показательной форме.

Решение.     1) = = .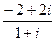

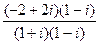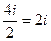2) Построим чертёж, найдём модуль и аргумент каждого из 2 чисел.

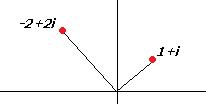
Модули ищутся по теореме Пифагора и равны 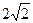 и .

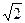Аргументы: , .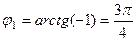

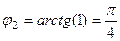Итак,  .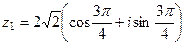

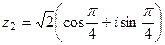Делим их модули и вычитаем аргументы.

 =  =

 = . 

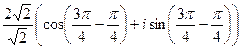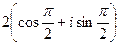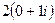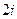3) =  =  = =  =

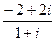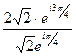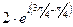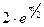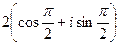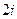
Ответ.  .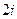

 

Задача 4. Умножить 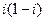 тремя способами:

1) с помощью обычного раскрытия скобок.

2) в тригонометрической форме.

3) в показательной форме.

Решение.   1)  =  = .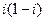

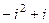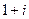2) Построим чертёж и найдём тригонометрическую форму каждого из чисел.

 

.

 

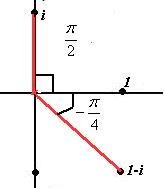
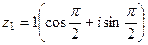
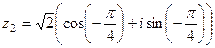Умножаются их модули и складываются аргументы.

 =  =

 = .

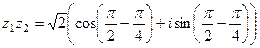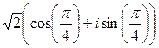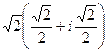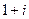3) 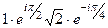  = 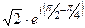 = 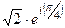, а далее раскроем по формуле Эйлера  =  = .

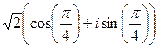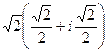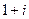Ответ. .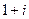 

 

 

Задача 5. Вычислить в показательной форме .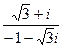

Решение.

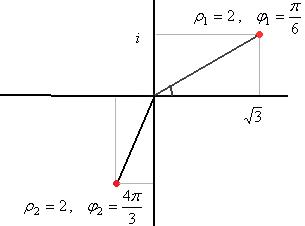
Для 1-го числа: 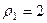,  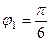.   Для 2-го: , .  

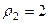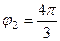Тогда 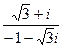 =  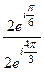=  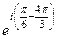=  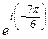= 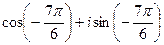, прибавим 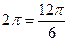, для удобства вычисления. Итак,  = .

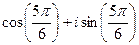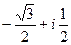Ответ. .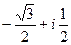

Дом. задание. Задачу 5 можно самостоятельно решить без показательной формы, умножением на сопряжённое.

Задача 6. Возвести в степень: .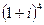

Решение. Перейдём к показательной форме, для этого сначала найдём модуль и аргумент числа 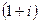 с помощью чертежа. Число в 1-й четверти, угол 45 градусов.

Чертёж, показывающий, расположение 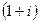 на плоскости, это число выделено красным цветом:

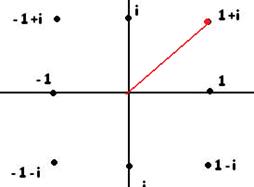
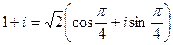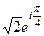 = . По формуле Муавра,  =

 = =  =  =  = . 

 

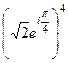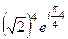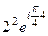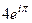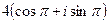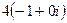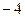Ответ. .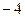 

Задача 7. Возвести в степень в показательной форме: .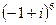

Решение.    Сначала построим чертёж и найдём 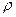 и .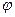

 

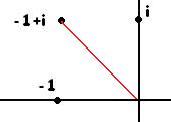
По чертежу видно, что угол здесь на 45 град. меньше чем 180, то есть 135 градусов, то есть 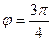, Проекции красной линии на координатные оси имеют длину 1 (каждая), поэтому 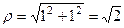. Тогда ,  =

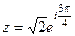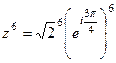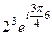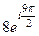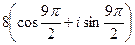=  = , мы можем отбросить 1 или более полных оборотов, при этом синус и косинус не изменятся, то есть отнять 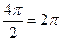, либо 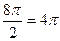. Тогда угол  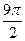эквивалентен 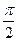, и остаётся вычислить:  =  = .

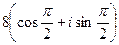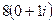Ответ .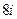

 

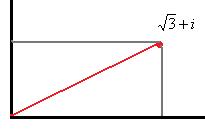
Задача 8. Возвести в степень .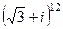    

Решение. Аналогично прошлой задаче, сначала переводим в показательную форму. Угол здесь 30 градусов, то есть 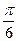, модуль 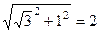. Итак,  = .

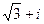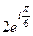Тогда  =  =  =  =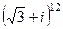

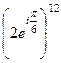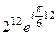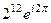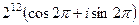
Теперь можем отнять полный оборот 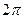 , косинус и синус при этом не меняются. тогда получим  =  = 

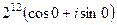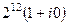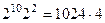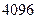 = . Ответ. .

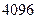Домашняя задача. Как в задаче 8, возвести в степень 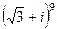.   Ответ.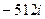

Задача 9. Вычислить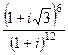

Решение. Представим каждое число в показательной форме.

 , , , .

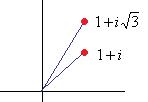
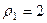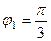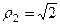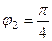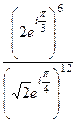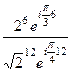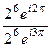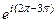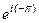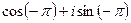 = =  =  =  =  но можно произвольно прибавить 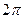, ведь от этого не изменятся синус и косинус, поэтому

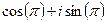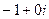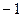=  = .        Ответ. .

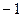Задача 10. Вычислить  .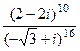 

Решение. Представим в показательной форме каждое из чисел.

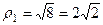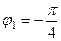,   и 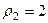, 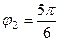. Тогда

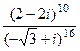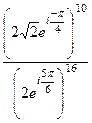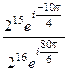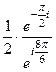 =  =  =  здесь в числителе прибавили угол 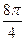, кратный 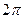, а в знаменателе отняли 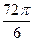. Далее,  =  =  =  =  =  = .

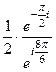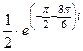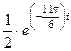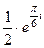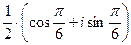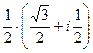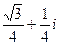Ответ. .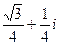

 

Домашняя задача.  Вычислить 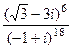. Ответ.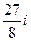

Практика 2 (неделя с 7 по 13 сентября).