Задача № 1. Найти решение задачи Коши для дифференциального уравнения первого порядка.
Вариант 0. 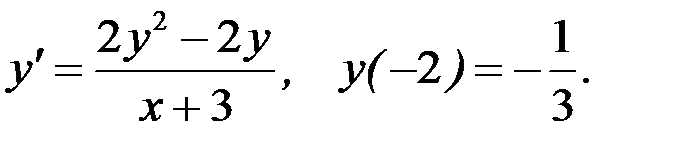
Вариант 1. 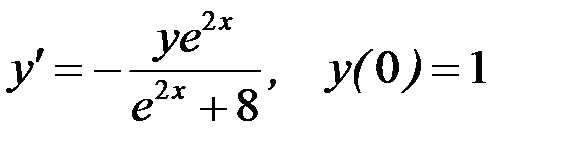 .
.
Вариант 2. 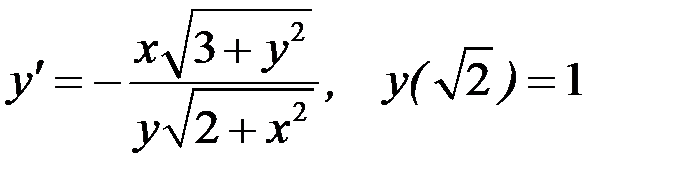 .
.
Вариант 3. 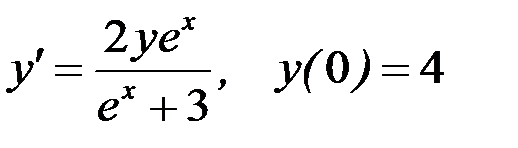 .
.
Вариант 4. 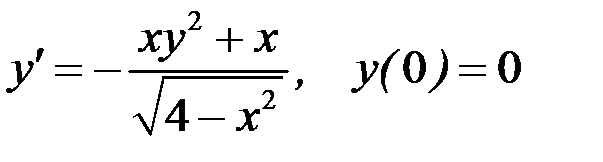 .
.
Вариант 5. 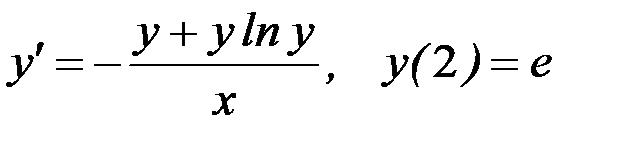 .
.
Вариант 6. 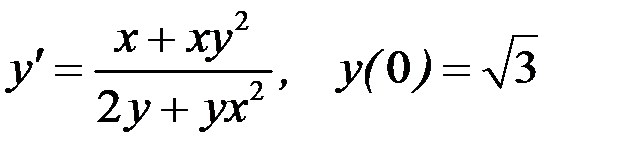 .
.
Вариант 7. 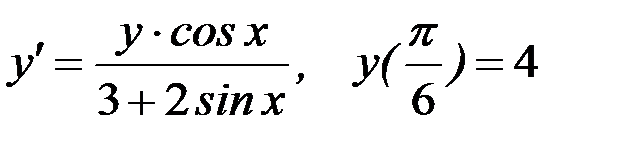 .
.
Вариант 8. 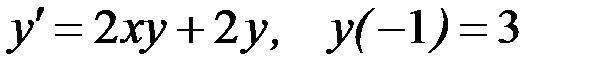 .
.
Вариант 9. 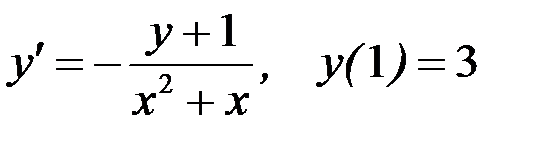 .
.
Задача № 2. Найти общее решение дифференциального уравнения.
Вариант 0.  а)
а) 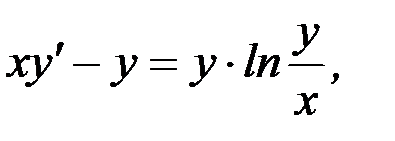
 б)
б) 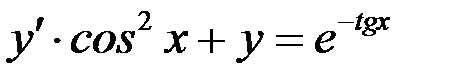 .
.
Вариант 1.  а)
а) 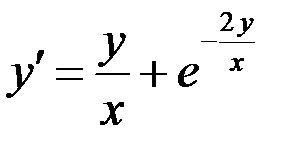 ,
,  б)
б) 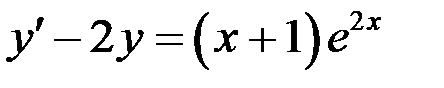 .
.
Вариант 2.  а)
а) 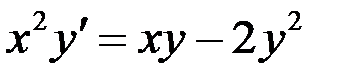 ,
,  б)
б) 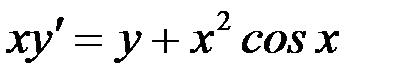 .
.
Вариант 3.  а)
а) 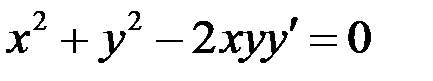 ,
,  б)
б) 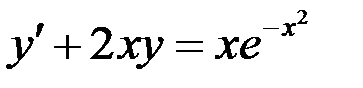 .
.
Вариант 4.  а)
а) 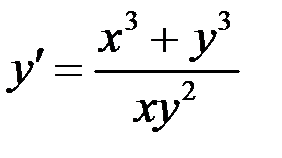 ,
,  б)
б) 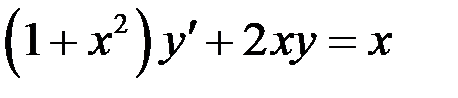 .
.
Вариант 5.  а)
а) 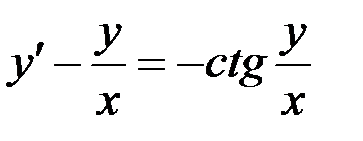 ,
,  б)
б) 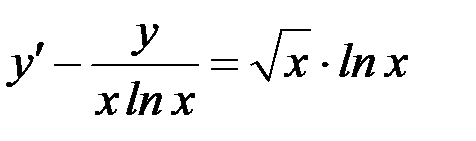 .
.
Вариант 6.  а)
а) 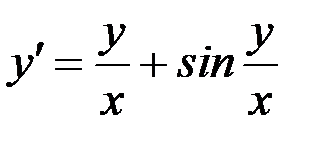 ,
,  б)
б) 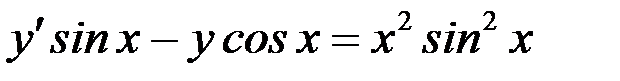 .
.
Вариант 7.  а)
а) 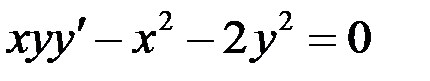 ,
,  б)
б) 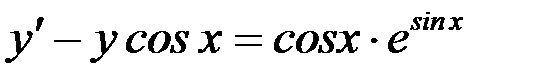 .
.
Вариант 8.  а)
а) 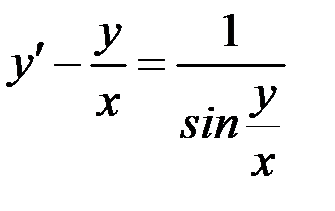 ,
,  б)
б) 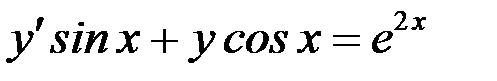 .
.
Вариант 9.  а)
а) 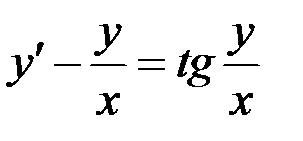 ,
,  б)
б) 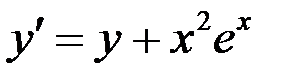 .
.
Задача № 3. Найти решение задачи Коши для линейного однородного дифференциального уравнения второго порядка.
Вариант 1. 

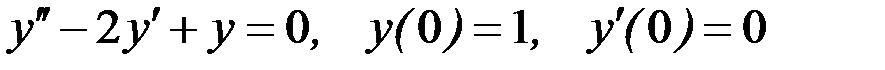 .
.
Вариант 2. 

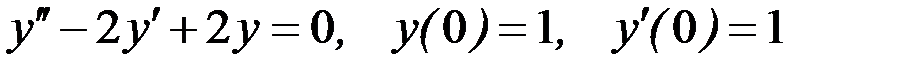 .
.
Вариант 3. 

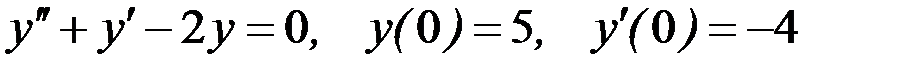 .
.
Вариант 4. 
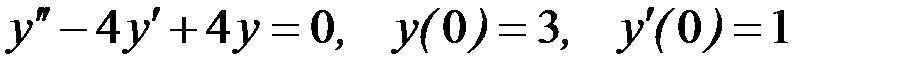 .
.
Вариант 5. 
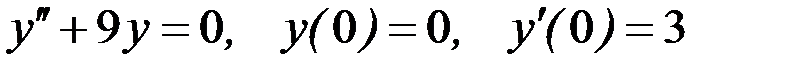 .
.
Вариант 6. 
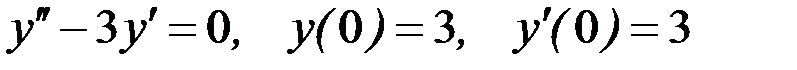 .
.
Вариант 7. 
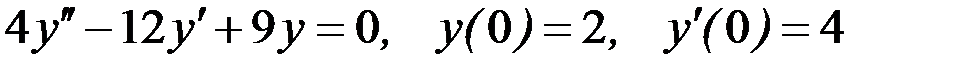 .
.
Вариант 8. 
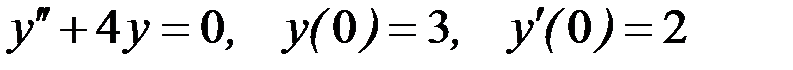 .
.
Вариант 9. 
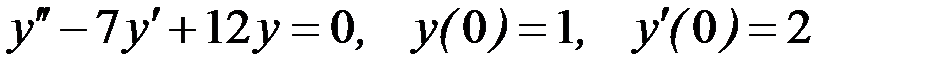 .
.
Вариант 10. 

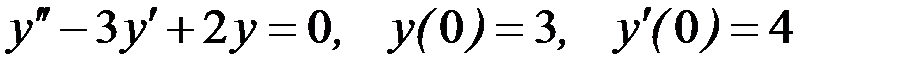 .
.
Задача № 4. Найти общее решение линейного дифференциального уравнения второго порядка
Вариант 1. 
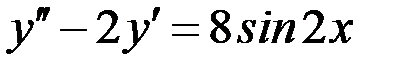 .
.
Вариант 2. 
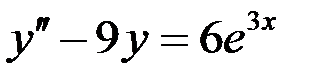 .
.
Вариант 3. 
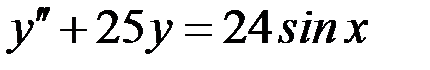 .
.
Вариант 4. 
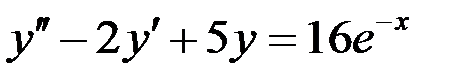 .
.
Вариант 5. 
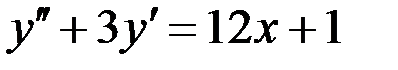 .
.
Вариант 6. 
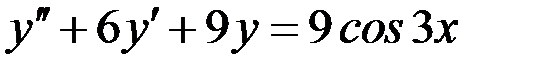 .
.
Вариант 7. 
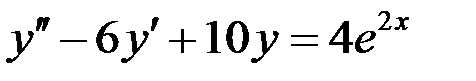 .
.
Вариант 8. 
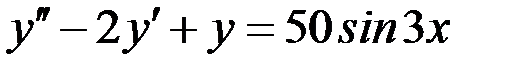 .
.
Вариант 9. 
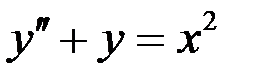 .
.
Вариант 10. 
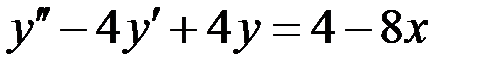 .
.
РЯДЫ
Практическая часть
Пример 8.1. Пользуясь одним из признаков сходимости числовых рядов с положительными членами, установить, сходится или расходится ряд 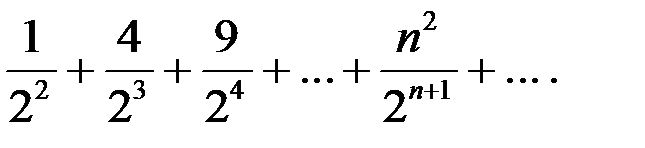
Решение. Применим к данному ряду с положительными членами признак Даламбера. Выпишем 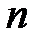 –й и
–й и 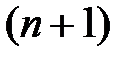 –й члены ряда:
–й члены ряда:
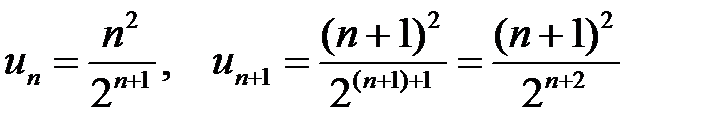 .
.
Тогда
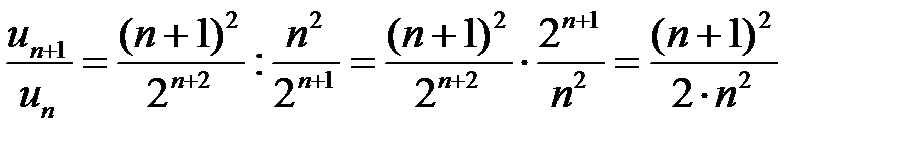 .
.
Вычислим предел 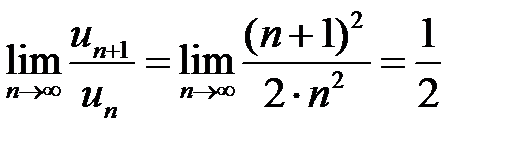 .
.
Так как 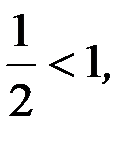 то данный ряд сходится.
то данный ряд сходится.
Пример 8.2. Установить, сходится или расходится знакочередующийся ряд
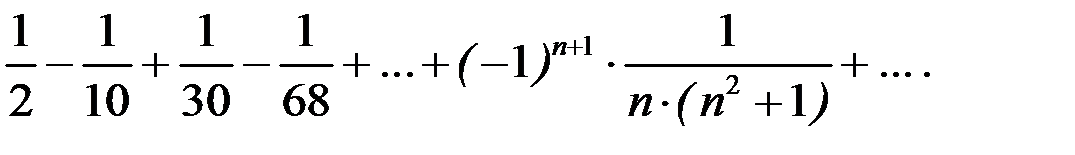
Если ряд сходится, то выяснить, как он сходится: абсолютно или условно.
Решение. Воспользуемся признаком Лейбница сходимости знакочередующегося ряда. Для данного в задаче ряда условия признака Лейбница выполнены:
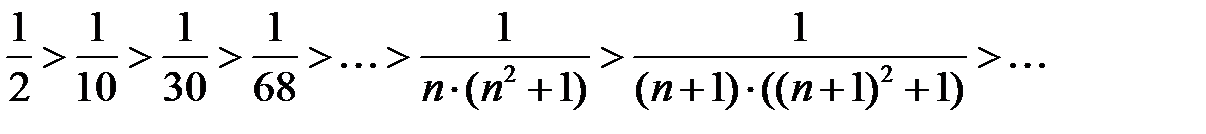
и
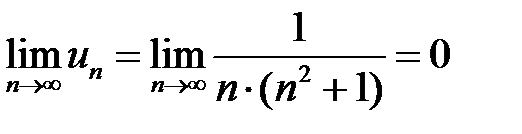 .
.
Следовательно, знакочередующийся ряд сходится. В этом случае он сходится либо абсолютно, либо условно.
Установим вид сходимости (абсолютная или условная) знакочередующегося ряда.
По исследуемому знакочередующемуся ряду
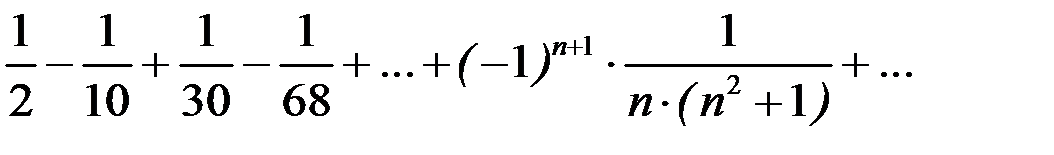
составим ряд из абсолютных величин его членов
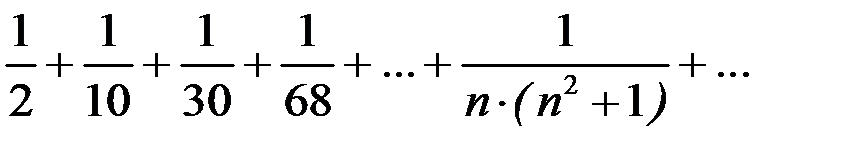 .
.
Последний ряд является числовым рядом с положительными членами. Применим к нему предельный признак сравнения. В качестве эталонного ряда выберем ряд
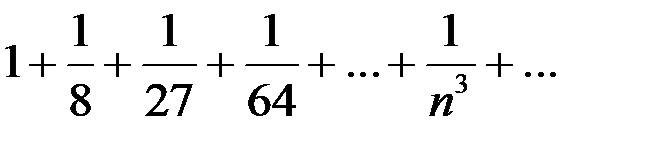 ,
,
который является обобщенным гармоническим рядом с 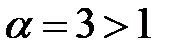 (это сходящийся ряд).
(это сходящийся ряд).
Так как
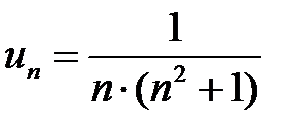 ,
, 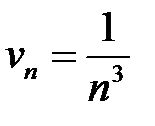 ,
,
то
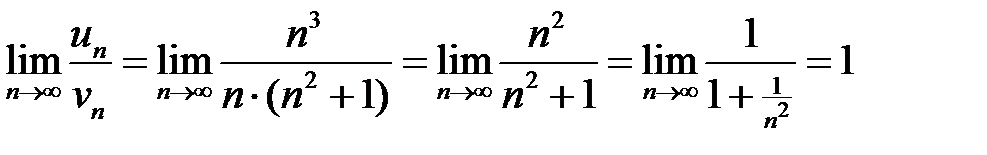 .
.
Получили, что 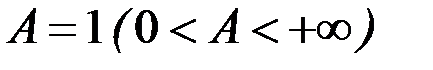 . Согласно предельному признаку сравнения оба ряда ведут себя одинаково. Отсюда следует, что ряд, составленный из абсолютных величин, сходится. Следовательно, исходный знакочередующийся ряд сходится абсолютно.
. Согласно предельному признаку сравнения оба ряда ведут себя одинаково. Отсюда следует, что ряд, составленный из абсолютных величин, сходится. Следовательно, исходный знакочередующийся ряд сходится абсолютно.
Пример 8.3. Найти область сходимости степенного ряда
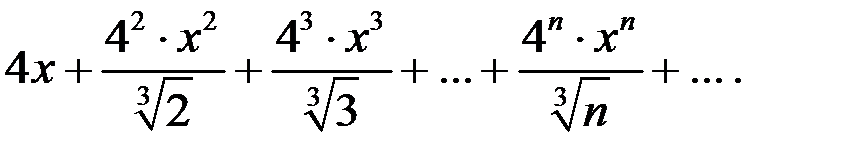
Решение. Найдем радиус сходимости степенного ряда по формуле 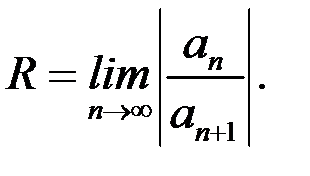 В данной задаче
В данной задаче
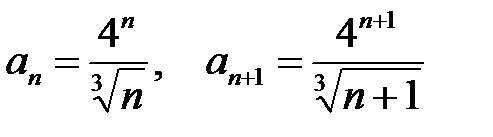 ,
,
поэтому
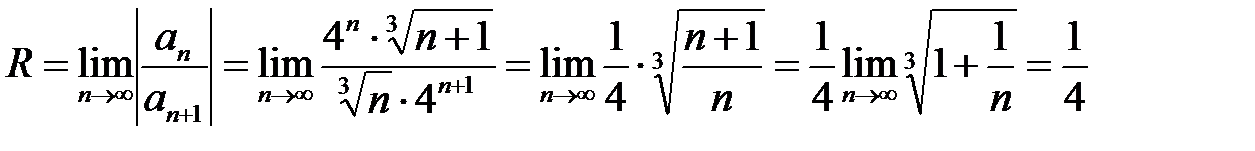 .
.
Следовательно, данный степенной ряд абсолютно сходится при 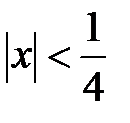 (то есть при
(то есть при 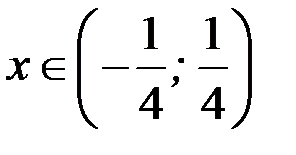 ) и расходится при
) и расходится при 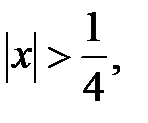 а интервал
а интервал 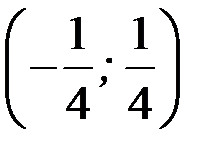 является интервалом сходимости этого ряда.
является интервалом сходимости этого ряда.
Исследуем сходимость ряда на концах интервала сходимости.
При 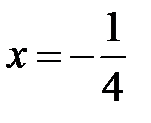 получаем знакочередующийся ряд
получаем знакочередующийся ряд
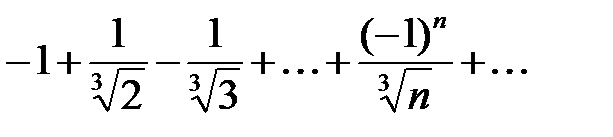 .
.
Для этого ряда проверим выполнение двух условий признака Лейбница.
Сравним 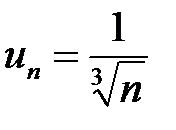 и
и 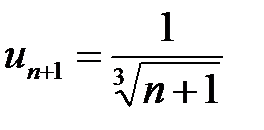 . Так как
. Так как 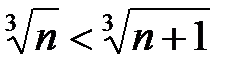 при всех натуральных значениях
при всех натуральных значениях 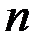 , то
, то 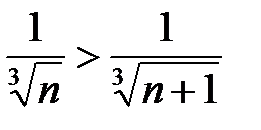 (
(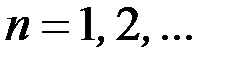 ). Следовательно, первое условие признака Лейбница выполнено.
). Следовательно, первое условие признака Лейбница выполнено.
Так как 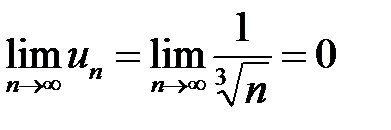 , то второе условие признака Лейбница также выполнено.
, то второе условие признака Лейбница также выполнено.
По признаку Лейбница знакочередующийся ряд сходится.
При 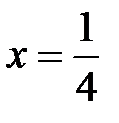 данный степенной ряд превращается в числовой ряд с положительными членами
данный степенной ряд превращается в числовой ряд с положительными членами
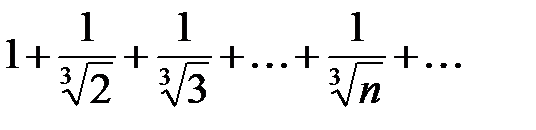 ,
,
который является обобщенным гармоническим рядом с 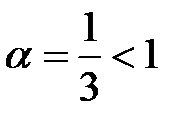 и, следовательно, расходится.
и, следовательно, расходится.
Таким образом, промежуток 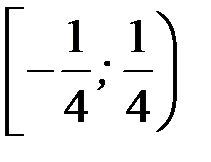 является областью сходимости исходного степенного ряда.
является областью сходимости исходного степенного ряда.
Пример 8.4. Пользуясь одним из разложений элементарных функций в ряд Маклорена, вычислить значение 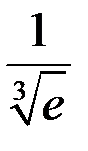 с точностью до 0,001.
с точностью до 0,001.
Решение. Воспользуемся разложением
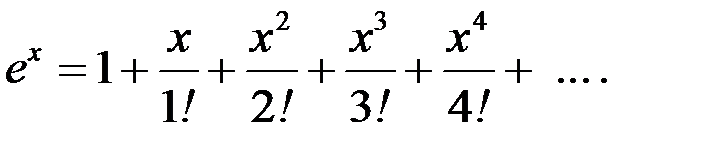
Полагая 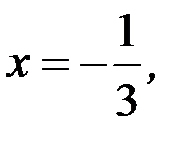 получаем:
получаем:
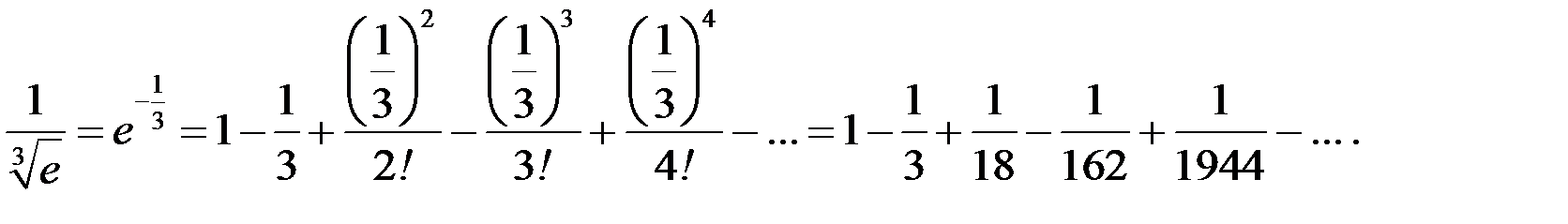
Так как последний знакочередующийся ряд удовлетворяет условиям теоремы Лейбница и 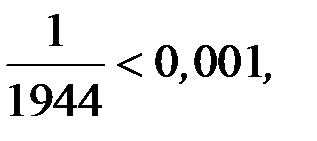 то, согласно замечанию 13.5, для приближенного вычисления значения
то, согласно замечанию 13.5, для приближенного вычисления значения 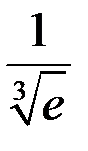 с точностью до 0,001 можно ограничиться первыми четырьмя членами ряда, отбросив все последующие члены этого ряда:
с точностью до 0,001 можно ограничиться первыми четырьмя членами ряда, отбросив все последующие члены этого ряда:
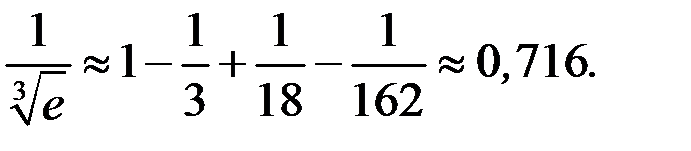
Пример 8.5. Вычислить 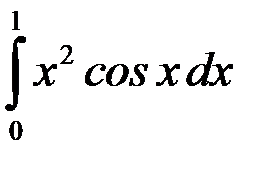 с точностью до 0,001, разложив в ряд Маклорена подынтегральную функцию.
с точностью до 0,001, разложив в ряд Маклорена подынтегральную функцию.
Решение. Воспользуемся разложением функции 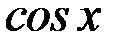 в ряд Маклорена:
в ряд Маклорена:
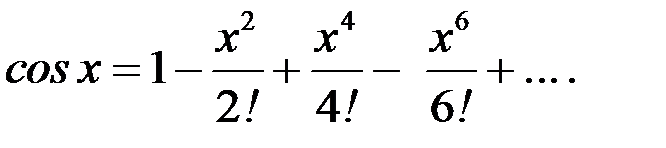
Тогда
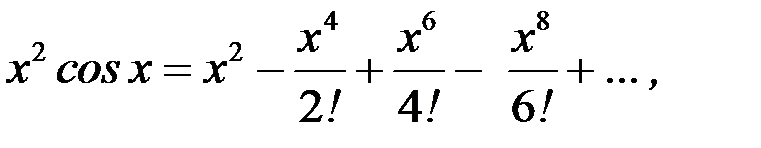
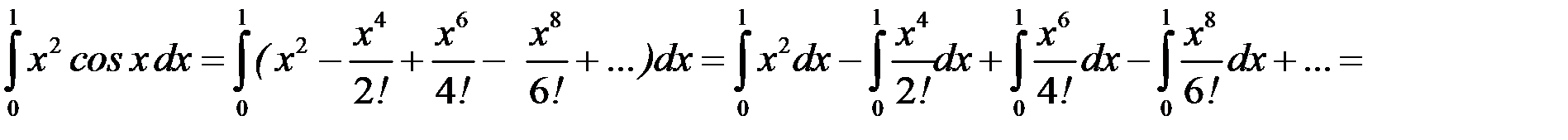
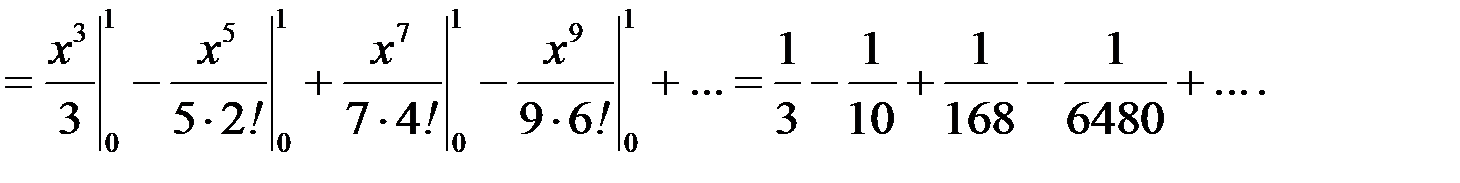
Так как последний ряд удовлетворяет условиям теоремы Лейбница и 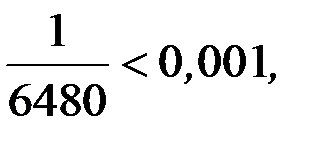 то для приближенного вычисления значения
то для приближенного вычисления значения 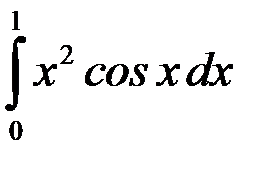 с точностью до 0,001 можно ограничиться первыми тремя членами ряда, отбросив все последующие члены этого ряда:
с точностью до 0,001 можно ограничиться первыми тремя членами ряда, отбросив все последующие члены этого ряда:
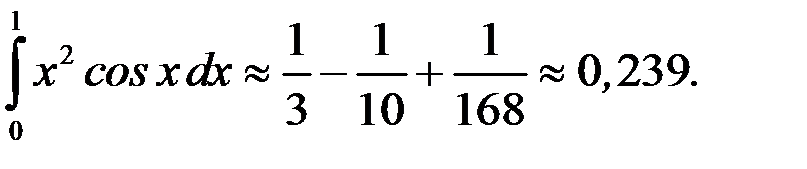
Пример 8.6. Найти три первых, отличных от нуля, члена разложения в степенной ряд функции, являющейся решением дифференциального уравнения 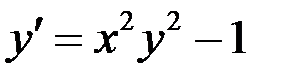 при условии, что
при условии, что 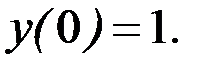
Решение. Будем искать решение 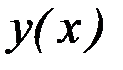 в виде ряда Маклорена:
в виде ряда Маклорена:
9. 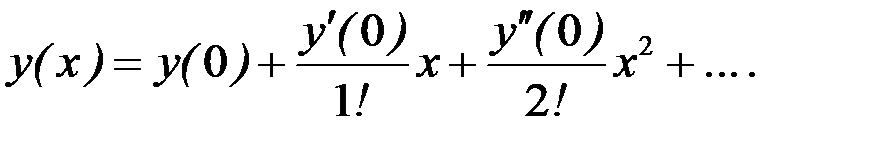
Подставляя в данное дифференциальное уравнение первого порядка начальные условия 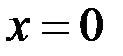 и
и 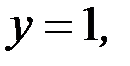 находим, что
находим, что 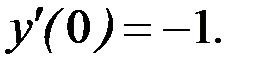 Продифференцируем обе части исходного уравнения по переменной
Продифференцируем обе части исходного уравнения по переменной 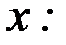
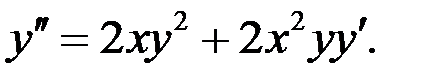 При
При 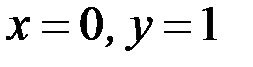 и
и 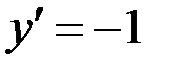 получим
получим 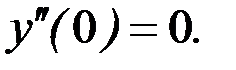 Дифференцируем предыдущее уравнение:
Дифференцируем предыдущее уравнение:
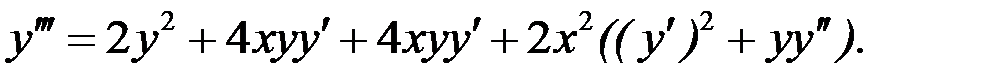
Используя начальные условия, получаем 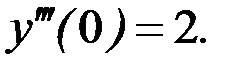
Подставляя найденные значения производных в ряд Маклорена, получаем: 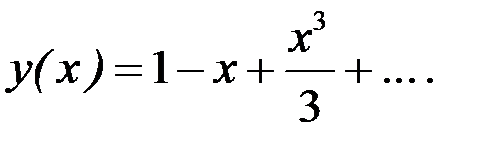
 2020-10-09
2020-10-09 150
150








