2020-10-09
376
Для нахождения точек пересечения графика с осью 
решим систему уравнений
Отсюда получаем, что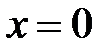 
, 
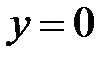. Следовательно, точка 
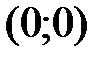является точкой пересечения графика функции с осью 
.
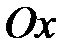Для нахождения точки пересечения графика функции с осью 
решим систему уравнений
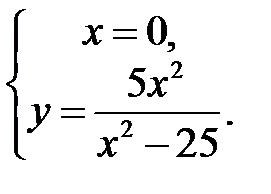
Отсюда 
, 
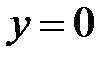, поэтому точка 
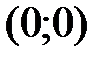является точкой пересечения графика функции с осью .
4. Исследование функции по первой производной (интервалы монотонности, точки экстремума).
Найдем первую производную функции:
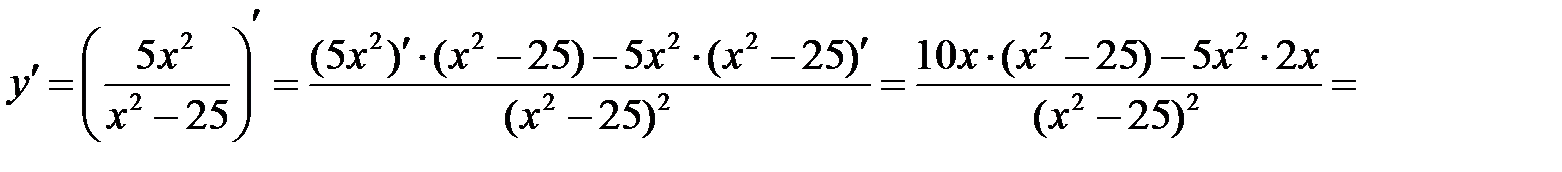
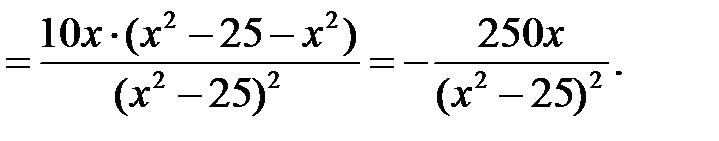
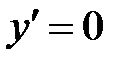при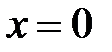 
, 
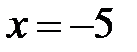не существует при 
и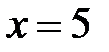 
. Точки 
, 
, 
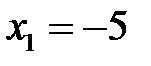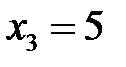разбивают область определения функции на четыре интервала 
, 
, 
, 
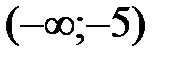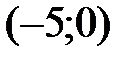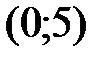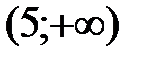. Определим знак производной 
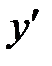на каждом из них. Возьмем любое число из интервала 
, например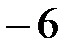 
. Так как 
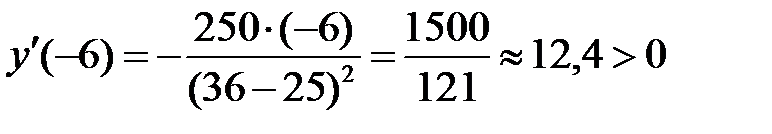, поэтому на всем интервале 
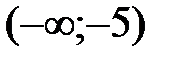производная 
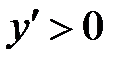и, следовательно, функция монотонно возрастает. Аналогично определяем знак производной 
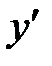на трех других интервалах:
,
,
.
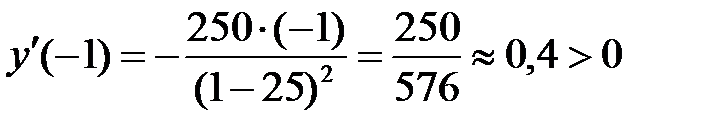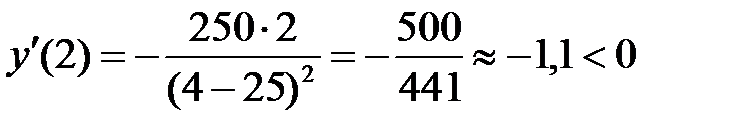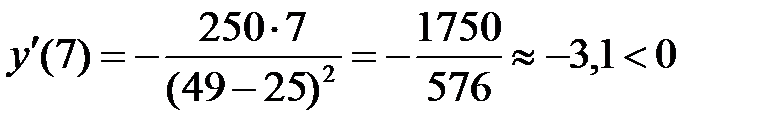Результаты исследования занесем в таблицу:
| 
| 
| 0 | 
| 
|
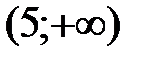
| + | + | 0 | − | − |
| 
| 0 | |||
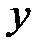
| функция возрастает | функция возрастает | max | функция убывает | функция убывает |
Итак, функция возрастает на каждом из интервалов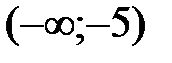 
, 
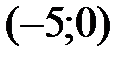и убывает на интервалах 
, 
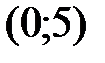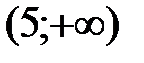. В точке 
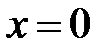производная меняет знак с «+» на «−», следовательно, 
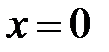− точка максимума функции. Значение функции в этой точке равно:
.
5. Исследование функции по второй производной (выпуклость, вогнутость, точки перегиба графика).
Найдем вторую производную функции:
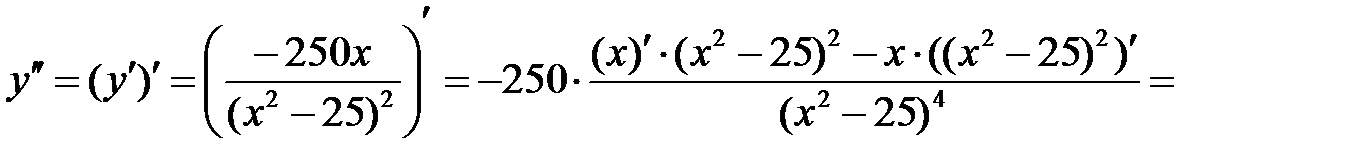
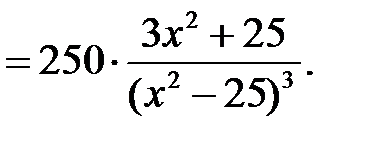
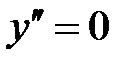, если 
. Это уравнение не имеет решения.
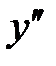не существует пр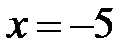и 
и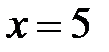 
.
Точки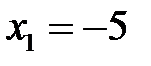 
, 
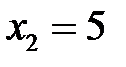разбивают область определения функции на три интервала: 
, 
, 
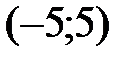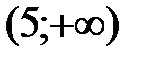. Определим знак производной 
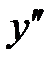на каждом из них. Так как 
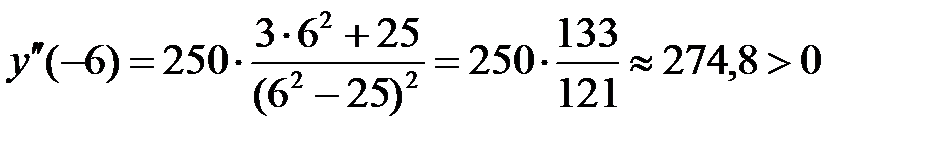, поэтому на всем интервале 
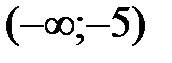производная 
и, следовательно, график функции является вогнутым на данном интервале. Аналогично определяем, что 
на интервале 
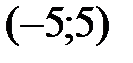, поэтому график выпуклый на данном интервале. На интервале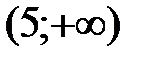 
, поэтому график вогнутый на этом интервале. Результаты исследования занесем в таблицу:
| 
| 
| 
|
| + | − | + |
| 
| 
|
|
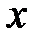
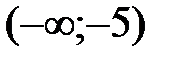
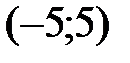
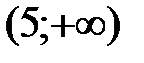
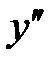
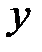
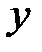
| вогнутый график | выпуклый график | вогнутый график |
Точек перегиба на графике функции нет.
