МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Методические указания к практическим занятиям
Для студентов по направлению подготовки
38.03.01 – Экономика
Воронеж 2016
УДК 512.8
Раецкая, Е. В. Математический анализ [Электронный ресурс]: методические указания к практическим занятиям для студентов по направлению подготовки 38.03.01 – Экономика / Е. В. Раецкая, И.В. Сапронов, Н.М. Спирина; М-во образования и науки РФ, ФГБОУ ВО «ВГЛТУ». – Воронеж, 2016.
Печатается по решению учебно-методического совета
ФГБОУ ВО «ВГЛТУ» (протокол № 5 от 22 апреля 2016 г.)
Рецензент д-р физ.-мат. наук, доцента кафедры математического анализа ВГУ Зубова С.П.
Введение
Целью изучения дисциплины «Математический анализ» является воспитание достаточно высокой математической культуры, привитие навыков современных видов математического мышления, обучение основным понятиям и методам математического анализа, необходимым для анализа и моделирования устройств, процессов и явлений при поиске оптимальных решений практических задач, методам обработки и анализа результатов численных экспериментов для экономических задач.
Основной задачей является выработка умения решать примеры и задачи для последующего применения математических методов в различных приложениях.
Студент по результатам освоения дисциплины «Математический анализ» должен обладать способностью выбрать инструментальные средства для обработки экономических данных в соответствии с поставленной задачей, проанализировать результаты расчетов и обосновать полученные выводы.
В результате освоения дисциплины студент должен:
- знать основные понятия, определения и методы исследования объектов с помощью теорем и формул различных разделов математического анализа;
- уметь: решать задачи и примеры по различным разделам высшей математики с доведением решения до практического приемлемого результата (формулы, числа, графика, качественного вывода и т.п.),
- уметь при решении задач выбирать необходимые вычислительные методы и средства (ПЭВМ, таблицы и справочники);
-самостоятельно изучать научную литературу по математике;
- иметь представление о численных алгоритмах решения математических и прикладных задач его профессиональной области.
ПРЕДЕЛ ФУНКЦИИ
Практическая часть
П р и м е р 1. Вычислить предел 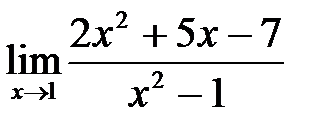 .
.
Решение. 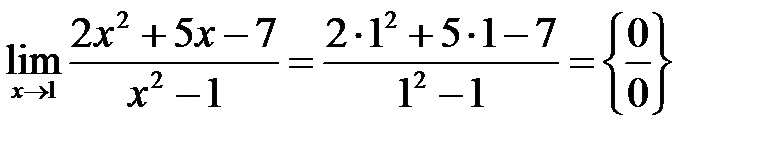 .
.
Получили неопределенность 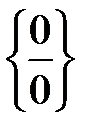 . Для раскрытия этой неопределенности необходимо, воспользовавшись формулами сокращенного умножения, разложить числитель и знаменатель дроби на множители, а затем сократить дробь на общий множитель, дающий в пределе ноль.
. Для раскрытия этой неопределенности необходимо, воспользовавшись формулами сокращенного умножения, разложить числитель и знаменатель дроби на множители, а затем сократить дробь на общий множитель, дающий в пределе ноль.
Для числителя воспользуемся формулой разложения квадратного трехчлена на множители 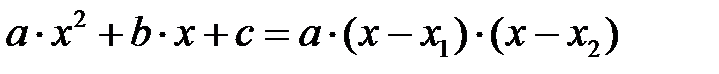 , где
, где 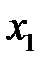 и
и 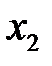 – корни квадратного трёхчлена. Получаем, что
– корни квадратного трёхчлена. Получаем, что
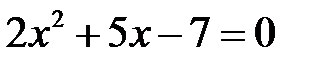
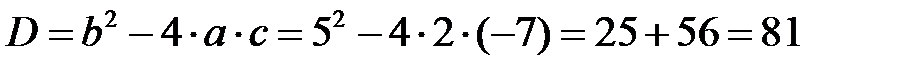
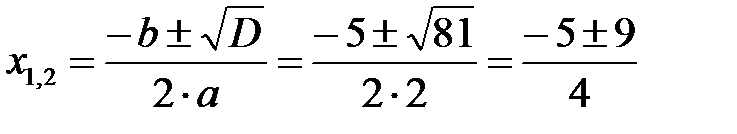
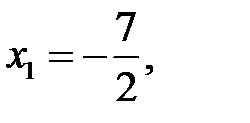
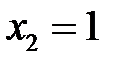 .
.
Следовательно,
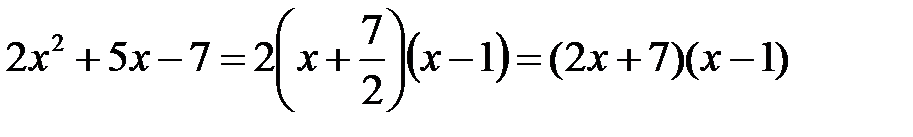 .
.
Знаменатель разложим, используя формулу разности квадратов 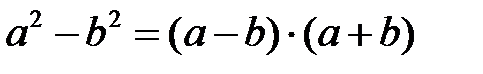 . Тогда
. Тогда 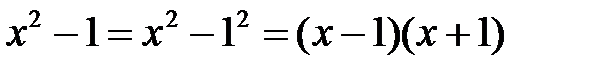 .
.
Имеем
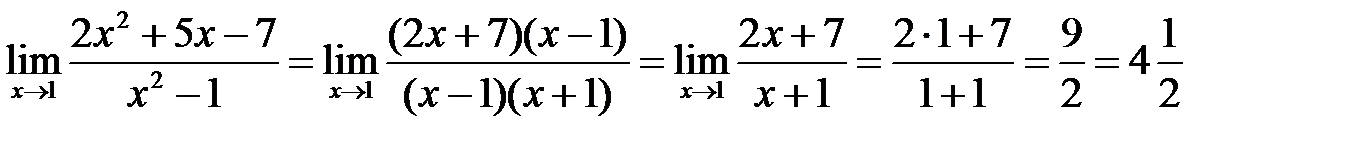 .
.
П р и м е р 2. Вычислить предел 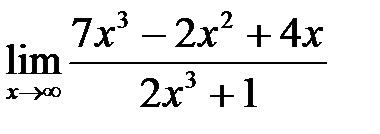 .
.
Решение. 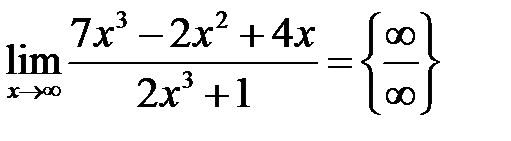 .
.
Получили неопределенность 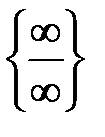 . Для раскрытия этой неопределенности нужно разделить числитель и знаменатель на
. Для раскрытия этой неопределенности нужно разделить числитель и знаменатель на 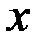 в старшей степени, т.е. на
в старшей степени, т.е. на 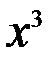 .
.
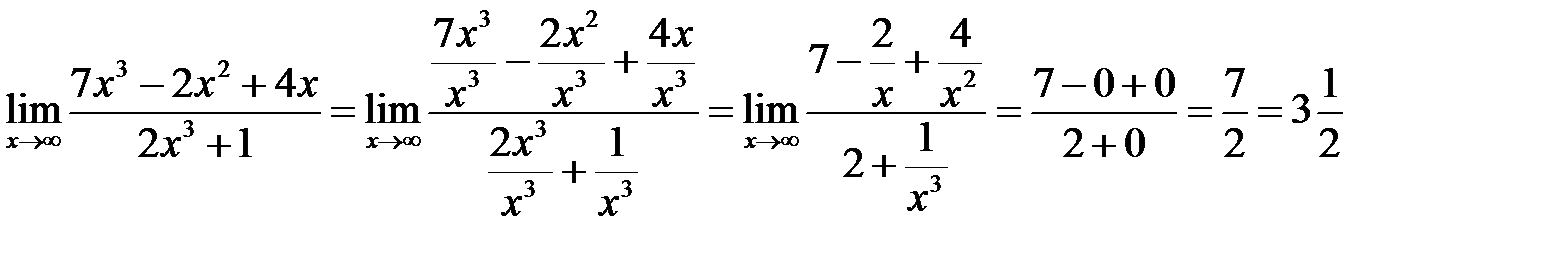 .
.
П р и м е р 3. Вычислить предел 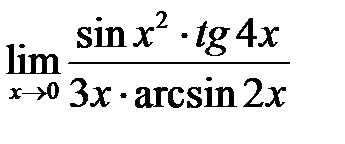 .
.
Решение. 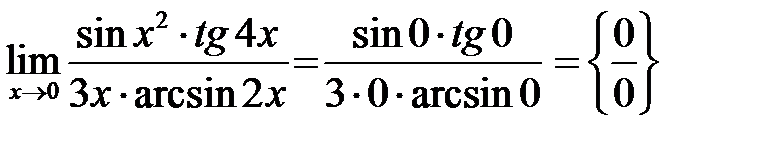 .
.
Получили неопределенность 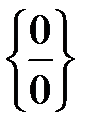 .
.
Выражение под знаком предела содержит тригонометрические функции, которые позволяют выделять первый замечательный предел, а именно,
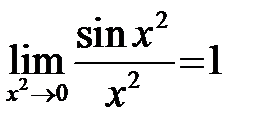 ,
, 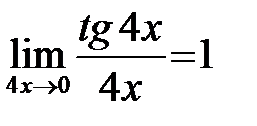 ,
, 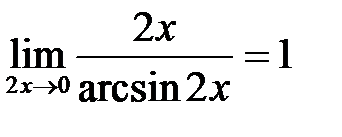 .
.
Домножив исходную дробь на дроби 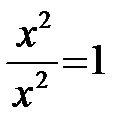 ,
, 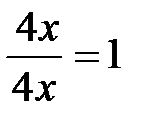 ,
, 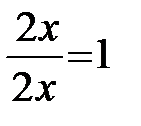 , выделим выражения для первых замечательных пределов из исходного выражения
, выделим выражения для первых замечательных пределов из исходного выражения

П р и м е р 4. Вычислить предел 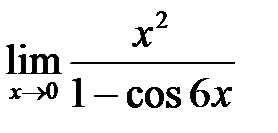 .
.
Решение. 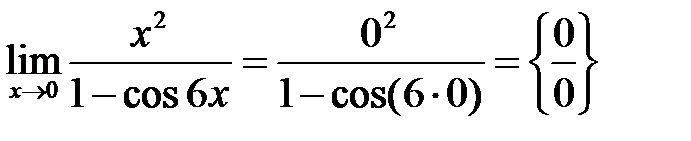 .
.
Получили неопределенность 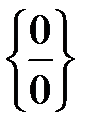 .
.
Сначала применим формулу 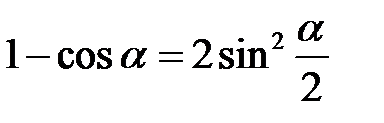 , а затем воспользуемся первым замечательным пределом
, а затем воспользуемся первым замечательным пределом 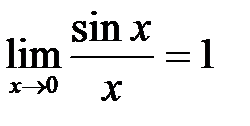 .
.
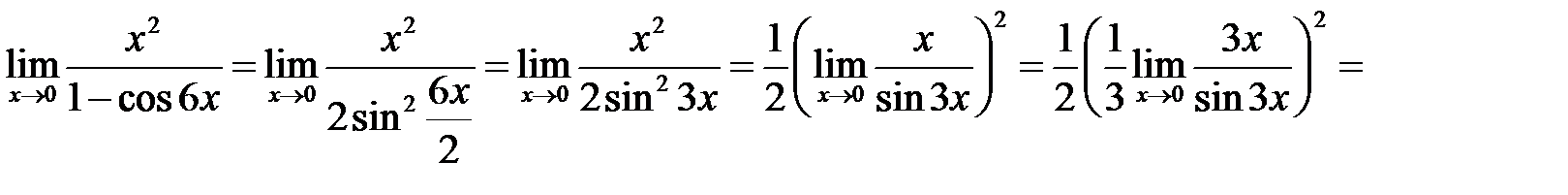
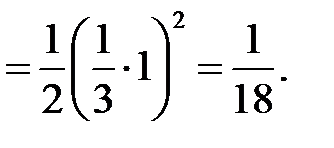
Индивидуальные задания
Вычислить пределы
1. а) 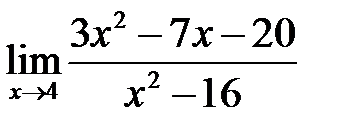 , б)
, б) 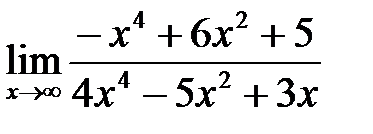 , в)
, в) 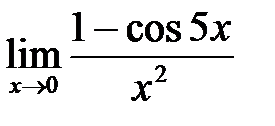 .
.
2. а) 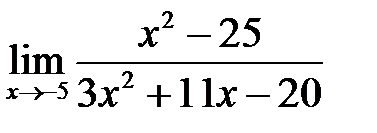 , б)
, б) 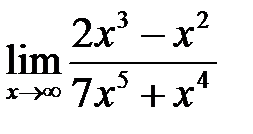 , в)
, в) 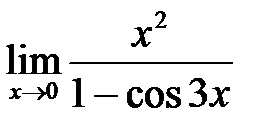 .
.
3. а) 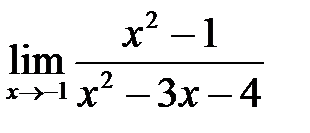 , б)
, б) 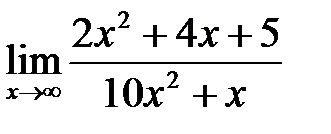 , в)
, в) 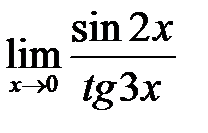 .
.
4. а) 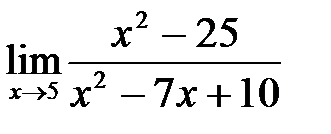 , б)
, б) 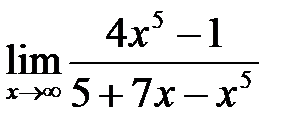 , в)
, в) 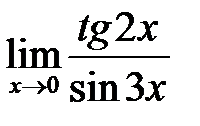 .
.
5. а) 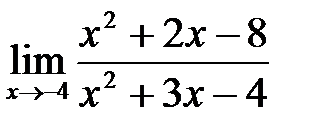 , б)
, б) 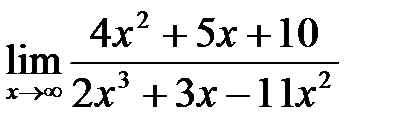 , в)
, в) 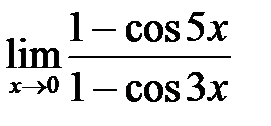 .
.
6. а) 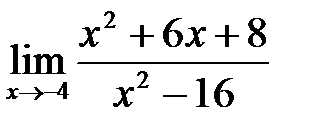 , б)
, б) 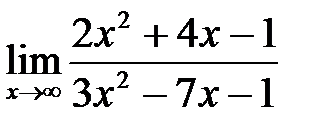 , в)
, в) 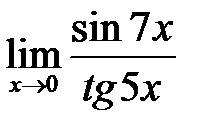 .
.
7. а) 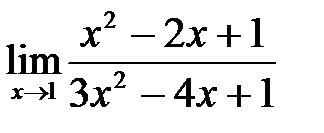 , б)
, б) 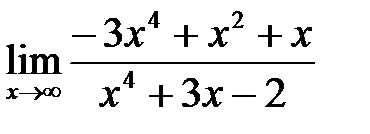 , в)
, в) 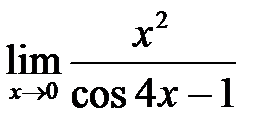 .
.
8. а) 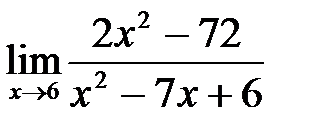 , б)
, б) 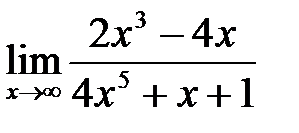 , в)
, в) 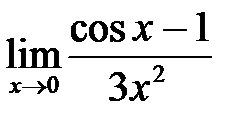 .
.
9. а) 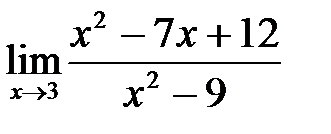 , б)
, б) 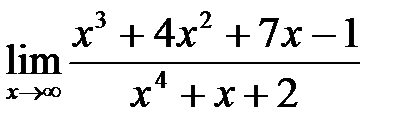 , в)
, в) 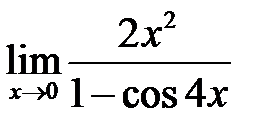 .
.
10. а) 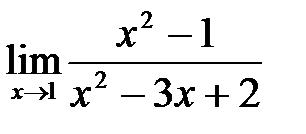 , б)
, б) 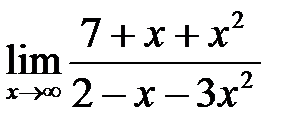 , в)
, в) 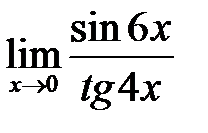 .
.
ПРОИЗВОДНАЯ ФУНКЦИИ
Практическая часть
П р и м е р 1. Найти производную функции 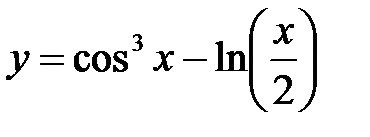 .
.
Решение. При нахождении производной используем
– таблицу производных основных элементарных функций;
– основные свойства производных;
– правило нахождения производной сложной функции.
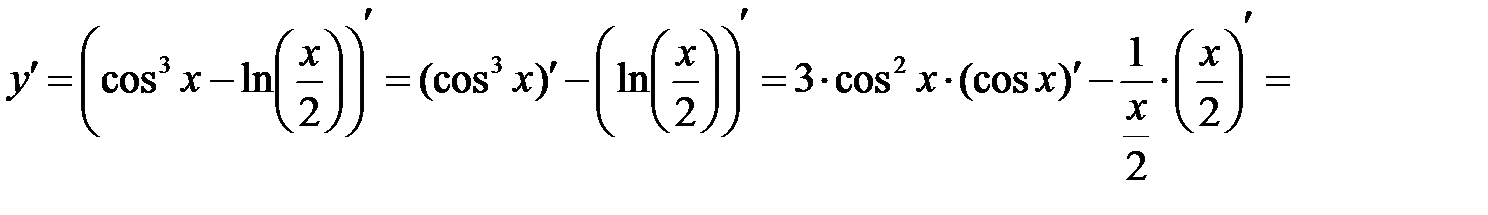
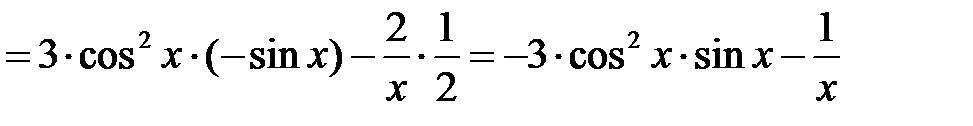 .
.
П р и м е р 2. Найти производную функции 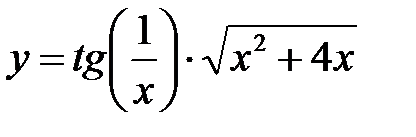 .
.
Решение. При нахождении производной используем
– таблицу производных основных элементарных функций;
– основные свойства производных;
– правило нахождения производной сложной функции.
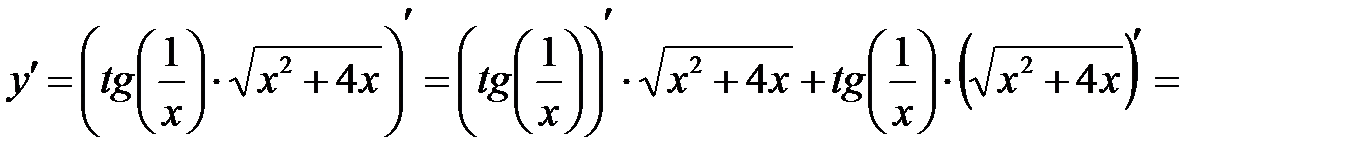
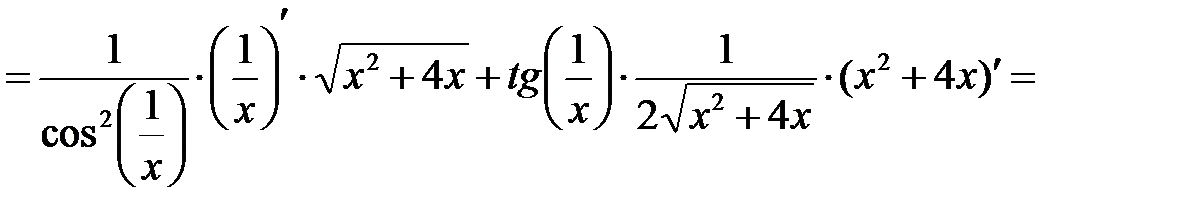
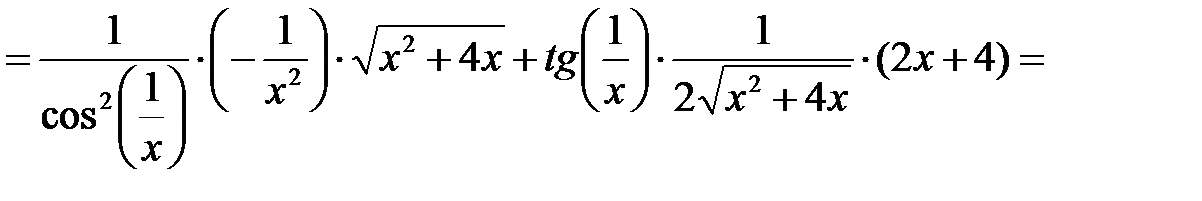
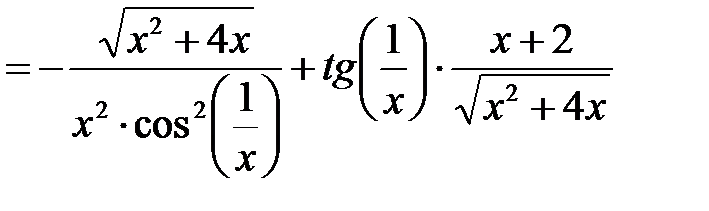 ;
;
П р и м е р 3. Найти производную функции 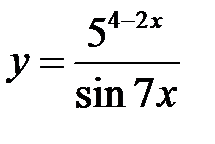 .
.
Решение. При нахождении производной используем
– таблицу производных основных элементарных функций;
– основные свойства производных;
– правило нахождения производной сложной функции.
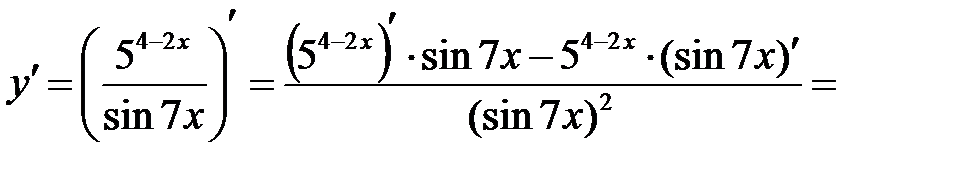
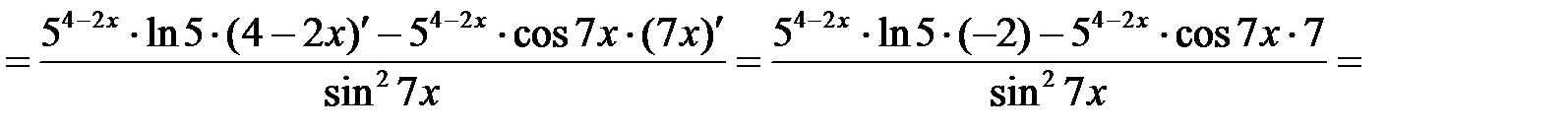
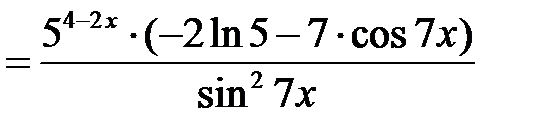 .
.
П р и м е р 4. Найти производную функции 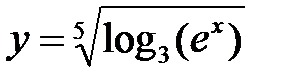 .
.
Решение. При нахождении производной используем
– таблицу производных основных элементарных функций;
– основные свойства производных;
– правило нахождения производной сложной функции.
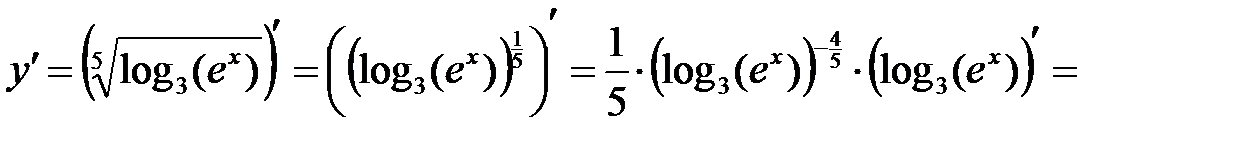
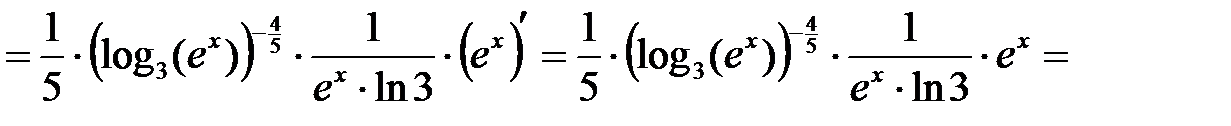
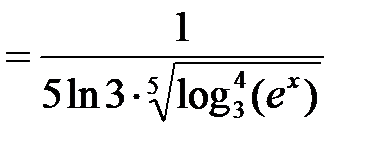 .
.
 2020-10-09
2020-10-09 236
236







