2020-10-09
180
Задание 1. Изобразить область определения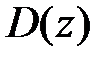 
функции двух переменных 
.
1.1. 
. 1.6. 
.
1.2. 
. 1.7. 
.
1.3. 
. 1.8. 
.
1.4. 
. 1.9. 
.
1.5. 
. 1.10. 
.
Задание 2. Найти частные производные функции двух переменных 2-го порядка.
2.1. а) 
; б) 
.
2.2. а) 
; б) 
.
2.3. а) 
; б) 
.
2.4. а) 
; б) 
.
2.5. а) 
; б) 
.
2.6. а) 
; б) 
.
2.7. а) 
; б) 
.
2.8. а) 
; б) 
.
2.9. а) 
; б) 
.
2.10. а) 
; б) 
.
Задание 3. Исследовать на экстремум функцию 
.
3.1. 
.
3.2. 
.
3.3. 
.
3.4. 
.
3.5. 
.
3.6. 
.
3.7. 
.
3.8. 
.
3.9. 
.
3.10. 
.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Практическая часть
Пример 1. Вычислить интеграл 
.
Преобразуем подынтегральную функцию:
.
Тогда 
= 
= 
== 
.
Пример 2. Вычислить интеграл 
.
Делаем замену 
, тогда 
и 
. Следовательно,
= 
= 
= 
.
Пример 3. Вычислить интеграл 
.
Делаем замену 
, тогда 
.
Следовательно,
= 
.
Пример 4. Вычислить интеграл 
.
Воспользуемся формулой интегрирования по частям:
.
.
Пример 5. Вычислить интеграл 
.
= 
.
Пример 6. Вычислить интеграл 
.
= 
= 
.
При решении мы воспользовались правилом 
Пример 7. Вычислить интеграл 
.
а) Знаменатель подынтегральной функции разложим на множители:
.
б) подынтегральную функцию представим в виде суммы простейших дробей:
.
Тогда
,
Следовательно,
.
Определим постоянные 
, 
и 
.
Если 
, то 
и 
;
если 
, то 
и 
;
если 
, то 
и 
.
Тогда
= 
= 
.
Индивидуальные задания
Вариант 0. 1) 
; 2) 
;
3) 
; 4) 
; 5) 
; 6) 
;
7) 
; 8) 
; 9) 
; 10) 
.
Вариант 1. 1) 
; 2) 
;
3) 
;
4) 
; 5) 
; 6) 
; 7) 
;
8) 
; 9) 
; 10) 
.
Вариант 2. 1) 
; 2) 
;
3) 
; 4) 
; 5) 
;
6) 
; 7) 
;
8) 
; 9) 
; 10) 
.
Вариант 3. 1) 
; 2) 
;
3) 
; 4) 
; 5) 
; 6) 
;
7) 
; 8) 
;
9) 
; 10) 
.
Вариант 4. 1) 
; 2) 
;
3) 
; 4) 
; 5) 
;
6) 
; 7) 
;
8) 
; 9) 
; 10) 
.
Вариант 5. 1) 
; 2) 
; 3) 
; 4) 
; 5) 
; 6) 
;
7) 
;
8) 
; 9) 
; 10) 
.
Вариант 6. 1) 
; 2) 
; 3) 
;
4) 
; 5) 
; 6) 
; 7) 
;
8) 
; 9) 
; 10) 
.
Вариант 7. 1) 
; 2) 
; 3) 
;
4) 
; 5) 
; 6) 
; 7) 
;
8) 
; 9) 
; 10) 
.
Вариант 8. 1) 
; 2) 
; 3) 
;
4) 
; 5) 
; 6) 
; 7) 
;
8) 
; 9) 
; 10) 
.
Вариант 9. 1) 
; 2) 
; 3) 
;
4) 
; 5) 
; 6) 
; 7) 
;
8) 
; 9) 
; 10) 
.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Практическая часть
Пример 1. Воспользуемся правилом интегрирования
,
табличным интегралом 1) и формулой Ньютона-Лейбница, получим:
= 
.
Пример 2. Воспользуемся методом интегрирования по частям для вычисления определённого интеграла:
= 
= 
= 
.
Пример 3. 
=
= 
= 
Пример 4. Воспользуемся правилом интегрирования (
) и табличным интегралом 4):
= 
Пример 5. Вычислить площадь фигуры, ограниченной линиями:
Рис.3
Найдём абсциссы точек пересечения графиков, заданных функций. Для этого объединим уравнения в систему
Решая полученную систему уравнений, получаем:
После построения графиков заданных функций получим фигуру (рис.3), ограниченную прямой 
и параболой 
.
Площадь фигуры, изображённой на рис.4, вычисляется по формуле:
.
В нашем случае 
, следовательно,
(кв. ед.).
Рис.4.
Пример 6. Вычислить объём тела, полученного при вращении вокруг оси 
фигуры, ограниченной линиями:
Первое уравнение задаёт гиперболу, а уравнение 
задаёт вертикальную прямую. После их построения, получаем фигуру, ограниченную гиперболой и вертикальной прямой. Пользуясь формулой для вычисления объёма тела вращения
,
находим объём тела (рис.5), образованного вращением нашей фигуры вокруг оси 
:
(куб. ед.)
Рис.5.
